题目内容
已知,D为CF上一点,AB∥CF,过E作直线交AB于B,交CF于C,
(1)若AE平分∠BAD,DE平分∠ADF,求证:AD=AB-CD.
(2)若AE平分∠BAD的外角,DE平分∠ADF的外角,求证:AD=CD-AB.

(1)若AE平分∠BAD,DE平分∠ADF,求证:AD=AB-CD.
(2)若AE平分∠BAD的外角,DE平分∠ADF的外角,求证:AD=CD-AB.

分析:(1)延长DE交AB于N,根据条件可以得出△ADE≌△ANE,进而可以得出△CDE≌△BNE,由全等三角形的性质就可以得出结论;
(2)延长AE交CD于N,由平行线的性质可以得出∠AED=90°,进而得出△ADE≌△NDE,就有AE=NE,可以得出△ABE≌△NCE,由全等三角形的性质就可以得出结论.
(2)延长AE交CD于N,由平行线的性质可以得出∠AED=90°,进而得出△ADE≌△NDE,就有AE=NE,可以得出△ABE≌△NCE,由全等三角形的性质就可以得出结论.
解答:解:(1)延长DE交AB于N,
∵AE平分∠BAD,DE平分∠ADF,
∴∠DAE=∠NAE=
∠DAN,∠ADE=
∠ADF.
∴∠DAE+∠ADE=
∠DAN+
∠ADF=
(∠DAN+∠ADF).
∵AB∥CF,
∴∠DAN+∠ADF=180°,∠C=∠B,∠CDE=∠BNE.
∴∠DAE+∠ADE=
×180°=90°
∴∠AED=∠AEN=90°
在△ADE和△ANE中,
∴△ADE≌△ANE(ASA),
∴AD=AN,DE=NE.
在△CDE和△BNE中,
,
∴△CDE≌△BNE(AAS),
∴CD=BN.
∵AN=AB-NB,
∴AD=AB-CD;
(2)延长BA到M,延长AE交CD于N,
∵AE平分∠DAM,DE平分∠ADC,
∴∠DAE=
∠DAM,∠ADE=∠NDE=
∠ADC,
∴∠DAE+∠ADE=
∠DAM+
∠ADC=
(∠DAM+∠ADC).
∵AB∥CF,
∴∠DAM+∠ADC=180°,∠C=∠B,∠CNE=∠BAE.
∴∠DAE+∠ADE=
×180=90.
∴∠AED=∠DEN=90°.
在△ADE和△NDE中
∴△ADE≌△NDE(ASA),
∴AD=DN,AE=NE.
在△ABE和△NCE中,
,
∴△ABE≌△NCE(AAS),
∴AB=NC.
∵DN=CD-CN,
∴AD=CD-AB.
∵AE平分∠BAD,DE平分∠ADF,
∴∠DAE=∠NAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE+∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CF,
∴∠DAN+∠ADF=180°,∠C=∠B,∠CDE=∠BNE.
∴∠DAE+∠ADE=
| 1 |
| 2 |
∴∠AED=∠AEN=90°
在△ADE和△ANE中,
|
∴△ADE≌△ANE(ASA),
∴AD=AN,DE=NE.
在△CDE和△BNE中,
|
∴△CDE≌△BNE(AAS),
∴CD=BN.
∵AN=AB-NB,
∴AD=AB-CD;
(2)延长BA到M,延长AE交CD于N,
∵AE平分∠DAM,DE平分∠ADC,
∴∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE+∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CF,
∴∠DAM+∠ADC=180°,∠C=∠B,∠CNE=∠BAE.
∴∠DAE+∠ADE=
| 1 |
| 2 |
∴∠AED=∠DEN=90°.
在△ADE和△NDE中
|
∴△ADE≌△NDE(ASA),

∴AD=DN,AE=NE.
在△ABE和△NCE中,
|
∴△ABE≌△NCE(AAS),
∴AB=NC.
∵DN=CD-CN,
∴AD=CD-AB.
点评:本题考查了角平分线的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,平行线的性质的运用,解答时求证三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
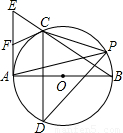
 如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE
如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE
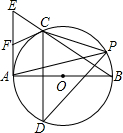
 如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE
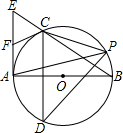
如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE ,连CP,求sin∠CPD的值.
,连CP,求sin∠CPD的值. ,连CP,求sin∠CPD的值.
,连CP,求sin∠CPD的值.