题目内容
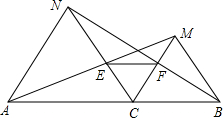 如图,A、C、B在一条直线上,△ACN、△BCM均为等边三角形,连结AM、BN交CN、CM于E、F点,连结EF.请提出一个结论,并证明.
如图,A、C、B在一条直线上,△ACN、△BCM均为等边三角形,连结AM、BN交CN、CM于E、F点,连结EF.请提出一个结论,并证明.考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:△ECF为等边三角形,理由为:由两三角形为等边三角形,利用等边三角形的性质得到AC=CN,BC=CM,∠ACN=∠BCM=60°,利用等式的性质得到夹角相等,利用SAS的三角形ACM与三角形NCB全等,利用全等三角形对应角相等得到一对角相等,利用ASA得到三角形ACE与三角形NCF全等,利用全等三角形对应边相等得到EC=FC,再利用一个角为60°的等腰三角形为等边三角形即可得证.
解答:解:△ECF为等边三角形,理由为:
∵△ACN和△BCM都为等边三角形,
∴AC=CN,BC=CM,∠ACN=∠BCM=60°,
∴∠ACN+∠NCM=∠BCM+∠MCN,即∠ACM=∠NCB,
在△ACM和△NCB中,
,
∴△ACM≌△NCB(SAS),
∴∠MAC=∠BNC,
在△ACE和△NCF中,
,
∴△ACE≌△NCF(ASA),
∴EC=FC,
则△ECF为等边三角形.
∵△ACN和△BCM都为等边三角形,
∴AC=CN,BC=CM,∠ACN=∠BCM=60°,
∴∠ACN+∠NCM=∠BCM+∠MCN,即∠ACM=∠NCB,
在△ACM和△NCB中,
|
∴△ACM≌△NCB(SAS),
∴∠MAC=∠BNC,
在△ACE和△NCF中,
|
∴△ACE≌△NCF(ASA),
∴EC=FC,
则△ECF为等边三角形.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
cosα表示的是( )
| A、一个角 | B、一个实数 |
| C、一个点 | D、一条射线 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长.
如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长.

 四边形ABCD是正方形,BE∥CG,∠AEB=60°,BC=CH=2
四边形ABCD是正方形,BE∥CG,∠AEB=60°,BC=CH=2