题目内容
⊙O的半径是20cm，圆心角∠AOB=120°，AB是⊙O弦，则S△AOB等于
- A.25
cm2 - B.50cm2
- C.100cm2
- D.200cm2
C
分析：先画出图形，过点O作OE⊥AB交AB于点E，在RT△AOE中，可求出OE、AE的长度，从而可求出S△AOB的值．
解答：
解：过点O作OE⊥AB交AB于点E，
由题意得，OA=OB=20cm，∠AOE=∠BOE=60°，
在RT△AOE中，OE=OAcos∠AOE=10cm，AE=AOsin∠AOE=10cm，
故可得AB=2AE=20cm
S△AOB=
AB×DE=100cm2．
故选C．
点评：此题考查了垂径定理及解直角三角形的性质，解答本题的关键是作出辅助线，求出OE及AE的长度，难度一般．
分析：先画出图形，过点O作OE⊥AB交AB于点E，在RT△AOE中，可求出OE、AE的长度，从而可求出S△AOB的值．
解答：
解：过点O作OE⊥AB交AB于点E，
由题意得，OA=OB=20cm，∠AOE=∠BOE=60°，
在RT△AOE中，OE=OAcos∠AOE=10cm，AE=AOsin∠AOE=10
cm，故可得AB=2AE=20
cmS△AOB=
AB×DE=100cm2．故选C．
点评：此题考查了垂径定理及解直角三角形的性质，解答本题的关键是作出辅助线，求出OE及AE的长度，难度一般．
练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
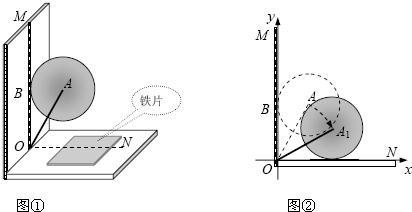轮切割水平放置的薄铁片（铁片厚度忽略不计，ON是切痕所在的直线）．
