题目内容
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.
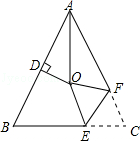

108。
如图,连接OB、OC,

∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO= ∠BAC=
∠BAC= ×54°=27°。
×54°=27°。
又∵AB=AC,∴∠ABC=(180°﹣∠BAC)=(180°﹣54°)=63°。
∵DO是AB的垂直平分线,∴OA=OB。
∴∠ABO=∠BAO=27°。∴∠OBC=∠ABC﹣∠ABO=63°﹣27°=36°。
∵DO是AB的垂直平分线,AO为∠BAC的平分线,
∴点O是△ABC的外心。∴OB=OC。∴∠OCB=∠OBC=36°。
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,∴OE=CE。
∴∠COE=∠OCB=36°。
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣36°﹣36°=108°。

∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=
 ∠BAC=
∠BAC= ×54°=27°。
×54°=27°。又∵AB=AC,∴∠ABC=(180°﹣∠BAC)=(180°﹣54°)=63°。
∵DO是AB的垂直平分线,∴OA=OB。
∴∠ABO=∠BAO=27°。∴∠OBC=∠ABC﹣∠ABO=63°﹣27°=36°。
∵DO是AB的垂直平分线,AO为∠BAC的平分线,
∴点O是△ABC的外心。∴OB=OC。∴∠OCB=∠OBC=36°。
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,∴OE=CE。
∴∠COE=∠OCB=36°。
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣36°﹣36°=108°。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目

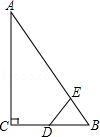
 ,则以a、b为边长的等腰三角形的周长为 .
,则以a、b为边长的等腰三角形的周长为 .