题目内容
解下列方程(组)
(1)
(2)
(3) .
.
解:(1) ,
,
2(2x-1)=3(x+2)+6,
4x-2=3x+6+6,
4x-3x=12+2
x=14;
(2)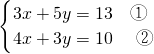 ,
,
把①×4-②×3得:
11y=22,
解得:y=2,
把y=2代入①得:x=1,
则原方程组的解是:
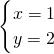 ;
;
(3)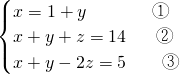 ,
,
②-③得:3z=9,
解得;z=3,
把①代入②得:
y=5,
把y=5代入①得:x=6,
则原方程组的解是: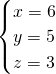 .
.
分析:(1)先在等式的两边同时乘以分母的最小公倍数,去掉分母,整理成一元一次方程,再求出x的值即可;
(2)先把原方程组进行变形,消去x,求出y的值,再把y的值代入①,求出x的值即可;
(3)先用②-③,求出z的值,再把①代入②,求出y的值,再把y,z的值代入①求出x的值即可.
点评:此题考查了解方程组,解题的关键是用到消元法,把三元一次方程组消到二元一次方程组,再把二元一次方程组消到一元一次方程,再进行求解.
 ,
,2(2x-1)=3(x+2)+6,
4x-2=3x+6+6,
4x-3x=12+2
x=14;
(2)
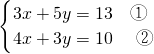 ,
,把①×4-②×3得:
11y=22,
解得:y=2,
把y=2代入①得:x=1,
则原方程组的解是:
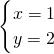 ;
;(3)
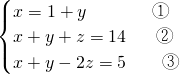 ,
,②-③得:3z=9,
解得;z=3,
把①代入②得:
y=5,
把y=5代入①得:x=6,
则原方程组的解是:
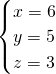 .
.分析:(1)先在等式的两边同时乘以分母的最小公倍数,去掉分母,整理成一元一次方程,再求出x的值即可;
(2)先把原方程组进行变形,消去x,求出y的值,再把y的值代入①,求出x的值即可;
(3)先用②-③,求出z的值,再把①代入②,求出y的值,再把y,z的值代入①求出x的值即可.
点评:此题考查了解方程组,解题的关键是用到消元法,把三元一次方程组消到二元一次方程组,再把二元一次方程组消到一元一次方程,再进行求解.

练习册系列答案
相关题目