题目内容
 已知关于x的一元二次方程x2-6x-k2=0(k为常数).
已知关于x的一元二次方程x2-6x-k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.
(1)证明:∵b2-4ac=(-6)2-4×1×(-k2)=36+4k2>0
因此方程有两个不相等的实数根.
(2)解:∵x1+x2=- =-
=-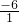 =6,
=6,
又∵x1+2x2=14,
解方程组 解得:
解得:
将x1=-2代入原方程得:(-2)2-6×(-2)-k2=0,
解得k=±4.
分析:(1)要证明方程有两个不相等的实数根,只要证明判别式△=b2-4ac的值大于0即可;
(2)根据一元二次方程的根与系数的关系可以得到两根的和是6,结合x1+2x2=14即可求得方程的两个实根,进而可求k的值.
点评:本题考查了一元二次方程根的判别式和根与系数的关系的应用,根据一元二次方程的根与系数的关系,与x1+2x2=14联立即可把求方程的解的问题转化为解方程组的问题.
因此方程有两个不相等的实数根.
(2)解:∵x1+x2=-
 =-
=-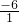 =6,
=6,又∵x1+2x2=14,
解方程组
 解得:
解得:
将x1=-2代入原方程得:(-2)2-6×(-2)-k2=0,
解得k=±4.
分析:(1)要证明方程有两个不相等的实数根,只要证明判别式△=b2-4ac的值大于0即可;
(2)根据一元二次方程的根与系数的关系可以得到两根的和是6,结合x1+2x2=14即可求得方程的两个实根,进而可求k的值.
点评:本题考查了一元二次方程根的判别式和根与系数的关系的应用,根据一元二次方程的根与系数的关系,与x1+2x2=14联立即可把求方程的解的问题转化为解方程组的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.