题目内容
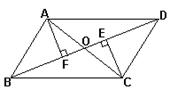
(每小题5分,共10分)已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17

试求:(1)AC的长; (2)四边形ABCD的面积;

试求:(1)AC的长; (2)四边形ABCD的面积;
(1)AC=15 (2)四边形ABCD的面积=114
分析:
(1)已知∠B=90°,则△ABC是直角三角形,根据勾股定理解答即可;
(2)根据△ACD的三边关系可判断出△ACD是直角三角形,再根据四边形ABCD面积=S△ABC+S△ACD计算。
解答:
(1)∵∠B=90°,
∴AC2= AB2+BC2=152
∴AC=15。
(2)∵AC2+AD2=CD2,
∴∠CAD=90°,
∴四边形ABCD面积=1/2×9×12+1/2×15×8=114。
点评:本题考查了利用勾股定理解直角三角形的能力及勾股定理的逆定理,比较简单。

练习册系列答案
相关题目






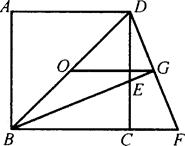
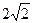 ,求正方形ABCD的面积.
,求正方形ABCD的面积.
 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少? ,
, ,那么梯形ABCD的周长是 .
,那么梯形ABCD的周长是 .