Question

如图，已知△ABC的顶点坐标为：A（-5，4），B（-3，1），C（-1，3）．
（1）画出△ABC关于直线x=2（记为Ⅲ）对称的图形△A′B′C′；
（2）点A关于直线m的对称点的坐标为______，点B′关于x轴的对称点的坐标为______；
（3）△A′B′C′的面积为______．

Answer 1

解：（1）如图所示：△A′B′C′为所画的图形


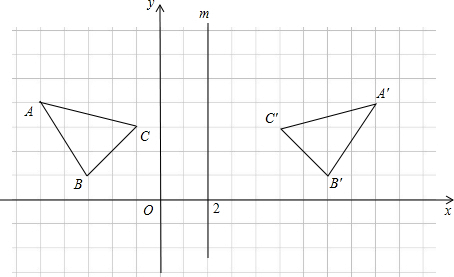
（2）点A关于直线m的对称点的坐标为（9，4），点B′关于x轴的对称点的坐标为（7，-1）．

（3）△A′B′C′的面积=4×3-×（2×2）-（2×3）-（1×4）=5．
故答案为：（9，4），（7，-1），5．
分析：（1）利用轴对称性质，作出△ABC的各个顶点关于直线Ⅲ的对称点，顺次连接，即得到关于直线Ⅲ轴对称的对应图形；
（2）根据图形即可得出答案；
（3）求△A′B′C′的面积即是求△ABC的面积，通过间接法即先求出该三角形所在的四边形的面积，后减去其旁边三个小三角形的面积即可求出．
点评：本题考查了轴对称变换作图，作轴对称后的图形的依据是轴对称的性质，基本作法是：①先确定图形的关键点；②利用轴对称性质作出关键点的对称点；③按原图形中的方式顺次连接对称点．