Question

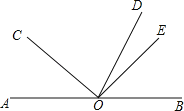
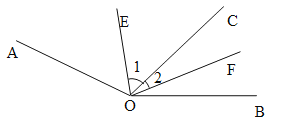
【题目】如图，，为其内部一条射线．

（1）若平分，平分.求的度数；

（2）若，射线从起绕着点顺时针旋转，旋转的速度是每秒钟，设旋转的时间为，试求当时的值．

Answer 1

【答案】（1）；（2）或，

【解析】

（1）根据角平分线定义和角的和差计算即可；

（2）分四种情况讨论：①当OM在∠AOC内部时，②当OM在∠BOC内部时，③当OM在∠AOB外部，靠近射线OB时，④当OM在∠AOB外部，靠近射线OA时．分别列方程求解即可．

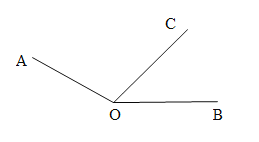
（1）∵OE平分∠AOC，OF平分∠BOC，

∴∠1=∠AOC，∠2=∠BOC，

∴∠EOF=∠1+∠2=∠AOC+∠BOC=(∠AOC+∠BOC)=∠AOB．

∵∠AOB=160°，

∴∠EOF=80°．

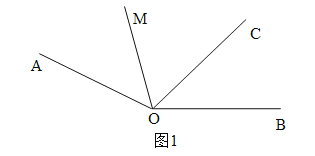
（2）分四种情况讨论：

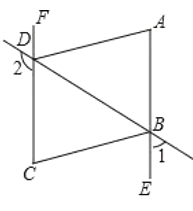
①当OM在∠AOC内部时，如图1．

∵∠AOC=100°，∠AOB=160°，

∴∠MOB=∠AOB-∠AOM=160°-．

∵∠AOM+∠MOC+∠MOB=∠AOC+∠MOB=200°，

∴100°+160°-=200°，

∴t=3．

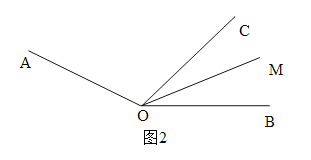
②当OM在∠BOC内部时，如图2．

∵∠AOC=100°，∠AOB=160°，

∴∠BOC=∠AOB-∠AOC=160°-100°=60°．

∵∠AOM+∠MOC+∠MOB=∠AOM+∠COB=200°，

∴，

∴t=7．

③当OM在∠AOB外部，靠近射线OB时，如图3，

∵∠AOB=160°，∠AOC=100°，

∴∠BOC=160°-100°=60°．

∵∠AOM=，

∴∠MOB=∠AOM-∠AOB=，∠MOC=．

∵∠AOM+∠MOC+∠MOB=200°，

∴，解得：t=．

∵∠AOB=160°，

∴OM转到OB时，所用时间t=160°÷20°=8．

∵＜8，

∴此时OM在∠BOC内部，不合题意，舍去．

④当OM在∠AOB外部，靠近射线OA时，如图4，

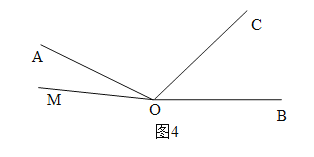
∵∠AOB=160°，∠AOC=100°，

∴∠BOC=160°-100°=60°．

∵，

∴∠MOC=∠AOM+∠AOC==，∠MOB=∠AOM+∠AOB==．

∵∠AOM+∠MOC+∠MOB=200°，

∴，解得：t=19．

当t=19时，=380°＞360°，则OM转到了∠AOC的内部，不合题意，舍去．

综上所述：t=3s或t=7s．