题目内容
 如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=
如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD=10°
10°
.分析:根据三角形的内角和等于180°求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后根据∠EAD=∠BAE-∠BAD代入数据进行计算即可得解.
解答:解:∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=
∠BAC=
×60°=30°,
∵AE是△ABC的高线,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAD=∠BAE-∠BAD=40°-30°=10°.
故答案为:10°.
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE是△ABC的高线,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAD=∠BAE-∠BAD=40°-30°=10°.
故答案为:10°.
点评:本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,是基础题,准确识图找出各角度之间的关系是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
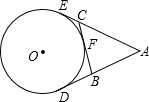 如图,AD、AE、BC都是⊙O的切线,切点分别为D、E、F,若AD=6,则△ABC的周长为
如图,AD、AE、BC都是⊙O的切线,切点分别为D、E、F,若AD=6,则△ABC的周长为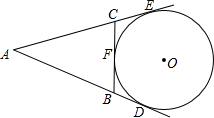 如图,AD、AE、CB都是⊙O的切线,切点分别为D、E、F,AD=4cm,则△ABC的周长是
如图,AD、AE、CB都是⊙O的切线,切点分别为D、E、F,AD=4cm,则△ABC的周长是 如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为( )
如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为( )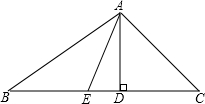 如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数. 如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.