题目内容
等边三角形绕某点旋转后能够与自身重合,则旋转角至少是
- A.60°
- B.90°
- C.120°
- D.180°
C
分析:先根据等边三角形的性质找到中心点,再根据旋转的定义求出旋转角至少要多少度(中心角度数).
解答: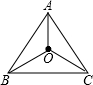 解:如图.
解:如图.
∵点O是等边△ABC的中心点;
∴∠AOB=∠AOC=∠BOC=120°;
∴由旋转的性质得出△AOB绕点O逆时针至少旋转120度后与△BOC重合.
故选C.
点评:等边三角形绕某点旋转后能够与自身重合,找到等边三角形的中心点,即旋转中心是解题的关键.
分析:先根据等边三角形的性质找到中心点,再根据旋转的定义求出旋转角至少要多少度(中心角度数).
解答:
 解:如图.
解:如图.∵点O是等边△ABC的中心点;
∴∠AOB=∠AOC=∠BOC=120°;
∴由旋转的性质得出△AOB绕点O逆时针至少旋转120度后与△BOC重合.
故选C.
点评:等边三角形绕某点旋转后能够与自身重合,找到等边三角形的中心点,即旋转中心是解题的关键.

练习册系列答案
相关题目