题目内容
【题目】如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB , 求∠BAB′的度数.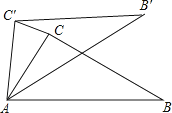
【答案】【解答】∵CC′∥AB ,
∴∠A CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
【解析】先根据平行线的性质,由CC′∥AB得∠ACC′=∠CAB=70°,再根据旋转的性质得AC=AC′,∠BAB′=∠CAC′,于是根据等腰三角形的性质有∠ACC′=∠AC′C=70°,然后利用三角形内角和定理可计算出∠CAC′=40°,从而得到∠BAB′的度数.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目