ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЪЕМљ
ВйзїЗЂЯжЃК
ШчЭМ1КЭЭМ2ЃЌвбжЊЕу![]() ЮЊе§ЗНаЮ
ЮЊе§ЗНаЮ![]() ЕФБп
ЕФБп![]() КЭ
КЭ![]() ЩЯЕФвЛИіЖЏЕуЃЈЕу
ЩЯЕФвЛИіЖЏЕуЃЈЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉЃЌзїЩфЯп
Г§ЭтЃЉЃЌзїЩфЯп![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
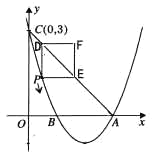
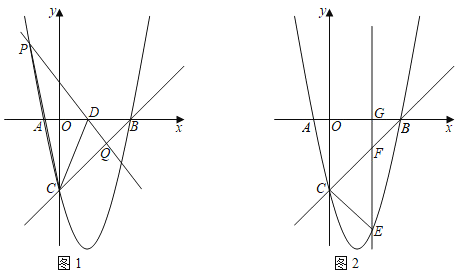
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉдЫЖЏЪБЃЌЧѓжЄЃК
Г§ЭтЃЉдЫЖЏЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
 ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ
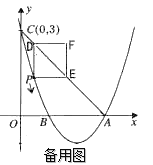
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕу![]() дк
дк![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉдЫЖЏЪБЃЌЧыжБНгаДГіЯпЖЮ
Г§ЭтЃЉдЫЖЏЪБЃЌЧыжБНгаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЛ
ЭиЙуЬНЫїЃК
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌевГігы![]() ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛ
ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛ
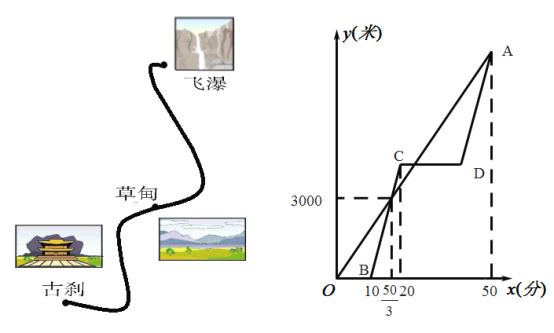
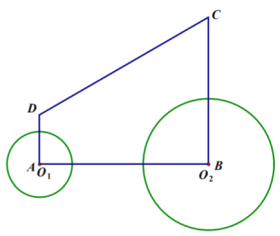
ЃЈ4ЃЉШчЭМ3ЃЌШєЕу![]() ЮЊОиаЮ
ЮЊОиаЮ![]() ЕФБп
ЕФБп![]() ЩЯвЛЕуЃЌзїЩфЯп
ЩЯвЛЕуЃЌзїЩфЯп![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЎШє
ЃЎШє![]()
![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() _______ЃЎ
_______ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉ
ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
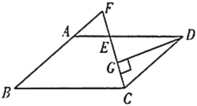
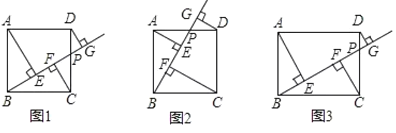
(1)зїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌЕУЕНЫФБпаЮDGFHЮЊОиаЮЃЌжЄЕУCF+ DG =CHЃЌЩшЗЈжЄЕУ![]() ЃЌЕУЕНAE=CHЃЌМДПЩжЄЕУНсТлЃЛ
ЃЌЕУЕНAE=CHЃЌМДПЩжЄЕУНсТлЃЛ
(2)вРее(1)ЕФЗНЗЈМДПЩЕУЕНCF = AE + DGЃЛ
(3)ИљОн(1)ЕФЗНЗЈжЄЕУ![]() ЃЌЕУЕНAE=BFЃЌBE=CFЃЌРћгУ(1)ЕФНсТлПЩЧѓЕУEF= DGЃЛ
ЃЌЕУЕНAE=BFЃЌBE=CFЃЌРћгУ(1)ЕФНсТлПЩЧѓЕУEF= DGЃЛ
(4)зїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌЕУЕНЫФБпаЮDGFHЮЊОиаЮЃЌЕУЕН DG= CH- CFЃЌИљОнвбжЊЬѕМўвзжЄЕУ![]() ЃЌПЩЧѓЕУ
ЃЌПЩЧѓЕУ![]() ЃЌ
ЃЌ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌПЩЕУЕН
ЃЌПЩЕУЕН![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЃЌМДПЩЧѓЕУНсТлЃЎ
ЃЌМДПЩЧѓЕУНсТлЃЎ
(1)Й§DзїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌШчЭМЃЌ
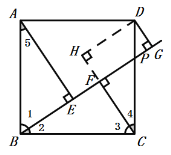
ЁпCFЁЭBGЃЌDGЁЭBGЃЌ
ЁрЫФБпаЮDGFHЮЊОиаЮЃЌ
ЁрDG=HFЃЌ
ЁрCF+ DG= CF+ HF =CHЃЌ
ЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌЧвAEЁЭBGЃЌ
ЁрAB=CDЃЌЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
ЁрЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌЁЯ2+ЁЯ3=90
ЃЌЁЯ2+ЁЯ3=90![]() ЃЌЁЯ3+ЁЯ4=90
ЃЌЁЯ3+ЁЯ4=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ4ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
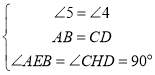 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=CHЃЌ
ЁрAE= CF+ DGЃЛ
(2)CF = AE + DGЃЛ
вРее(1)ЕФЗНЗЈЃЌШчЭМЃЌМДПЩжЄУїCF = AE + DGЃЛ
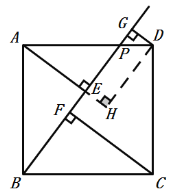
(3)EF= DGЃЌРэгЩШчЯТЃЌШчЭМЃК

гЩ(1)ЕУЃКЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ2ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
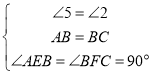 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=BFЃЌBE=CFЃЌ
ЁрEF=BF-BE=AE-CFЃЌ
ЁпAE= CF+ DGЃЌ
ЁрEF= DGЃЛ
(4)Й§DзїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌШчЭМЃЌ
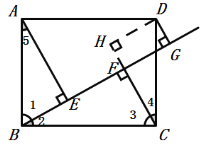
ЁпCFЁЭBGЃЌDGЁЭBGЃЌ
ЁрЫФБпаЮDGFHЮЊОиаЮЃЌ
ЁрDG=HFЃЌ
ЁрDG= CH- CFЃЌ
ЁпЫФБпаЮABCDЮЊОиаЮЃЌAEЁЭBGЃЌCD=2BE=6ЃЌ
ЁрAB=CD=2BE =6ЃЌBE =3ЃЌЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
ЁрЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌЁЯ2+ЁЯ3=90
ЃЌЁЯ2+ЁЯ3=90![]() ЃЌЁЯ3+ЁЯ4=90
ЃЌЁЯ3+ЁЯ4=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ4=ЁЯ2=30![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ