题目内容
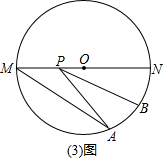
如图,在直角坐标系中,以AB为直径的⊙C交x轴于A,交y轴于B,满足OA:OB=4:3,以OC 为直径作⊙D,设⊙D的半径为2.
为直径作⊙D,设⊙D的半径为2.
(1)求⊙C的圆心坐标;
(2)过C作⊙D的切线EF交x轴于E,交y轴于F,求直线EF的解析式;
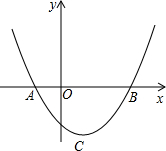
(3)抛物线y=ax2+bx+c(a≠0)的对称轴过C点,顶点在⊙C上,与y轴交点为B,求抛物线的解析式.
 为直径作⊙D,设⊙D的半径为2.
为直径作⊙D,设⊙D的半径为2.(1)求⊙C的圆心坐标;
(2)过C作⊙D的切线EF交x轴于E,交y轴于F,求直线EF的解析式;
(3)抛物线y=ax2+bx+c(a≠0)的对称轴过C点,顶点在⊙C上,与y轴交点为B,求抛物线的解析式.
(1)∵OA⊥OB,OA:OB=4:3,⊙D的半径为2
∴⊙C过原点,OC=4,AB=8
A点坐标为(
,0)B点坐标为(0,
)
∴⊙C的圆心C的坐标为(
,
)(3分)
(2)由EF是⊙D的切线,
∴OC⊥EF
∵CO=CA=CB
∴∠COA=∠CAO,∠COB=∠CBO
∴Rt△AOB∽Rt△OCE∽Rt△FCO
∴
=
,
=
∴OE=5,OF=
∴E点坐标为(5,0),F点坐标(0,
)
∴切线EF的解析式为y=-
x+
;(7分)
(3)①当抛物线开口向下时,由题意,得
抛物线顶点坐标为(
,
+4),
可得:-
=
,
=
,c=
∴a=-
,b=1,c=
,
∴y=-
x2+x+
;(10分)
②当抛物线开口向上时,
顶点坐标为(
,
-4),
可得:-
=
,
=-
,c=
,
∴y=
x2-4x+
;
综上所述,抛物线解析式为:
y=-
x2+x+
或y=
x2-4x+
.(12分)
注:其他解法参照以上评分标准评分
∴⊙C过原点,OC=4,AB=8
A点坐标为(
| 32 |
| 5 |
| 24 |
| 5 |
∴⊙C的圆心C的坐标为(
| 16 |
| 5 |
| 12 |
| 5 |
(2)由EF是⊙D的切线,
∴OC⊥EF
∵CO=CA=CB
∴∠COA=∠CAO,∠COB=∠CBO
∴Rt△AOB∽Rt△OCE∽Rt△FCO
∴
| OE |
| AB |
| OC |
| OA |
| OF |
| AB |
| OC |
| OB |
∴OE=5,OF=
| 20 |
| 3 |
∴E点坐标为(5,0),F点坐标(0,
| 20 |
| 3 |
∴切线EF的解析式为y=-
| 4 |
| 3 |
| 20 |
| 3 |
(3)①当抛物线开口向下时,由题意,得
抛物线顶点坐标为(
| 16 |
| 5 |
| 12 |
| 5 |
可得:-
| b |
| 2a |
| 16 |
| 5 |
| 4ac-b2 |
| 4a |
| 32 |
| 5 |
| 24 |
| 5 |
∴a=-
| 5 |
| 32 |
| 24 |
| 5 |
∴y=-
| 5 |
| 32 |
| 24 |
| 5 |
②当抛物线开口向上时,
顶点坐标为(
| 16 |
| 5 |
| 12 |
| 5 |
可得:-
| b |
| 2a |
| 16 |
| 5 |
| 4ac-b2 |
| 4a |
| 8 |
| 5 |
| 24 |
| 5 |
∴y=
| 5 |
| 8 |
| 24 |
| 5 |
综上所述,抛物线解析式为:
y=-
| 5 |
| 32 |
| 24 |
| 5 |
| 5 |
| 8 |
| 24 |
| 5 |
注:其他解法参照以上评分标准评分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






 88平方米?
88平方米?