题目内容
8.某数学课外实习小组想利用树影测量树高,他们在同一时刻测得一身高为1.5米的同学的影子长为1.35米,因大树靠近一栋建筑物,大树的影子不全在地面上,他们测得地面部分的影子长BC=3.6米,墙上影子高CD=1.8米,求树高AB.(根据题意画出草图并计算)分析 如图,BC=3.6m,CD=1.8m,作DE⊥AB于E,易得DE=BC=3.6,BE=CD=1.8,根据“在同一时刻物高与影长的比相等”得到$\frac{AE}{DE}$=$\frac{1.5}{1.35}$,再利用比例性质求出AE,然后计算AE与BE的和即可.
解答  解:如图,BC=3.6m,CD=1.8m,
解:如图,BC=3.6m,CD=1.8m,
作DE⊥AB于E,则DE=BC=3.6,BE=CD=1.8,
∵$\frac{AE}{DE}$=$\frac{1.5}{1.35}$,
∴AE=$\frac{1.5×3.6}{1.35}$=4,
∴AB=AE+BE=4+1.8=5.8(m),
答:树高AB为5.8m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
相关题目
19.下列说法正确的为( )
| A. | 如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互为补角 | |
| B. | 如果两个角相等,那么它们的余角也相等 | |
| C. | 有公共顶点且又相等的角是对顶角 | |
| D. | 直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离 |
16.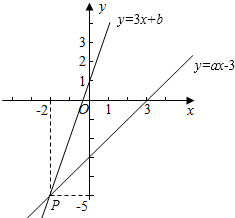 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )| A. | x>-2 | B. | x<-2 | C. | -2<x<0 | D. | x>0 |
3.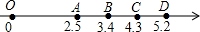 如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
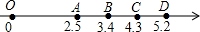 如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )
如图,在数轴上有标有O,A,B,C,D五个点,根据图中各点所表示的数,$\sqrt{12}$在线段( )| A. | OA上 | B. | AB上 | C. | BC上 | D. | CD上 |
17.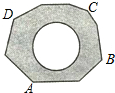 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
(1)当投掷的次数很大时,则m:n的值越来越接近0.5;
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下: | 50 | 50 | 300 | … |
| 石子落在圆内(含圆上)次数m | 14 | 48 | 89 | … |
| 石子落在圆以外的阴影部分(含外缘上)次数n | 30 | 95 | 180 | … |
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
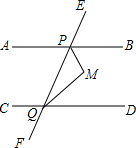 如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由.
如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由.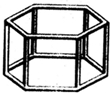 一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm,观察这个模型,回答下列问题:
一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm,观察这个模型,回答下列问题: