题目内容
如图,某城市有一条公路,从正西方向AO经过市中心,后转向北偏东30°方向OB.现要修建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.(1)若OA=OB=20km,求两出入口之间的距离;
(2)若OB=2OA,市中心O到高速公路L的距离为10km,求两出入口之间的距离;
(3)请你设计一种方案:确定两出入口的位置(两出入口到市中心O的距离不相等),使市中心到高速公路的距离扩大到12km.(不要求写出计算过程)

【答案】分析:(1)作OC⊥AB于C,在直角△AOC中根据三角函数求出AC,根据三线合一定理得到AB=2AC;
(2)作OC⊥AB于C,作BD⊥AO交AO的延长线于D,易证△AOC∽△ABD,根据相似三角形的对应边的比相等,就可以求出.
(3)答案不唯一:只要能够说出一组符合要求的OA和OB的长度即可.
解答: 解:(1)作OC⊥AB于C,
解:(1)作OC⊥AB于C,
∴∠ACO=∠BCO=90°.
∵OA=OB=20km∠AOB=120°,
∴∠CAO=∠CBO=30°.
∴OC= OA=10km.
OA=10km.
∴AC=BC= OC=10
OC=10 km.
km.
∴AB=20 km.
km.
答:两出入口之间的距离是20 km.
km.
(2)作OC⊥AB于C,作BD⊥AO交AO的延长线于D,
∴∠ACO=∠BCO=∠BDO=90°
∵∠AOB=120°
∴∠BOD=60°
∴∠OBD=90°-60°=30°
设OD=x则BD= x,
x,
∵OB=2OA,
∴OA=x则AD=AO+DO=2x AB= =
= x.
x.
∵∠A=∠A,
∴△AOC∽△ABD.
∴ =
= 即
即 =
= 解得x=
解得x= .
.
∴AB= x=
x=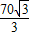 .
.
(3)答案不唯一:只要能够说出一组符合要求的OA和OB的长度即可,如取OA=15 km时,OB= km,
km,
(OA和OB的值大于12 km,且OA≠OB,先给出OA的值,然后求OB的值)不要求写出计算过程.
点评:本题主要考查解直角三角形的条件,已知直角三角形的一个锐角和一边长,或已知两边长就可以求出另外的边和角.
(2)作OC⊥AB于C,作BD⊥AO交AO的延长线于D,易证△AOC∽△ABD,根据相似三角形的对应边的比相等,就可以求出.
(3)答案不唯一:只要能够说出一组符合要求的OA和OB的长度即可.
解答:
 解:(1)作OC⊥AB于C,
解:(1)作OC⊥AB于C,∴∠ACO=∠BCO=90°.
∵OA=OB=20km∠AOB=120°,
∴∠CAO=∠CBO=30°.
∴OC=
 OA=10km.
OA=10km.∴AC=BC=
 OC=10
OC=10 km.
km.∴AB=20
 km.
km.答:两出入口之间的距离是20
 km.
km.(2)作OC⊥AB于C,作BD⊥AO交AO的延长线于D,

∴∠ACO=∠BCO=∠BDO=90°
∵∠AOB=120°
∴∠BOD=60°
∴∠OBD=90°-60°=30°
设OD=x则BD=
 x,
x,∵OB=2OA,
∴OA=x则AD=AO+DO=2x AB=
 =
= x.
x.∵∠A=∠A,
∴△AOC∽△ABD.
∴
 =
= 即
即 =
= 解得x=
解得x= .
.∴AB=
 x=
x=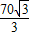 .
.(3)答案不唯一:只要能够说出一组符合要求的OA和OB的长度即可,如取OA=15 km时,OB=
 km,
km,(OA和OB的值大于12 km,且OA≠OB,先给出OA的值,然后求OB的值)不要求写出计算过程.
点评:本题主要考查解直角三角形的条件,已知直角三角形的一个锐角和一边长,或已知两边长就可以求出另外的边和角.

练习册系列答案
相关题目
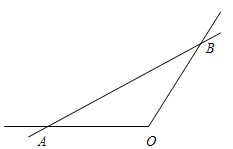 建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段. 建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
