题目内容
在平面直角坐标系 中,抛物线
中,抛物线 过点
过点 ,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为
,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为 ,连接CA,CB,CD.
,连接CA,CB,CD.
(1)求证: ;
;
(2) 是第一象限内抛物线上的一个动点,连接DP交BC于点E.
是第一象限内抛物线上的一个动点,连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出点E的坐标;
②连接CP,当△CDP的面积最大时,求点E的坐标.
(1)证明见解析;(2)(4,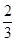 ),(6-
),(6-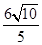 ,
,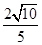 );(
);( ,
,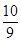 ).
).
解析试题分析:(1)把点(2,4)代入抛物线解析式计算即可求出m的值,然后求出点A、B、C的坐标,过点B作BM⊥CD交CD的延长线于M,然后求出∠CDO=∠BDM=45°,利用勾股定理列式分别求出CD、DM、BM,再根据锐角的正切相等证明即可;
(2)①利用勾股定理列式求出BC,再分BE=DE时,利用等腰三角形三线合一的性质求解,BE=BD时,利用∠OBC的正弦和余弦求解;
②根据抛物线解析式设出点P的坐标,过点P作x轴的垂线,垂足为F,交CD的延长线于点Q,再求出直线CD的解析式,然后写出点Q的坐标,再根据S△CDP=S△CPQ-S△DPQ列式整理,然后利用二次函数的最值问题求出点P的坐标,利用待定系数法求出直线PD的解析式,联立直线PD、BC的解析式,求解即可得到点E的坐标.
试题解析:(1)∵抛物线y=mx2+(m+2)x+2过点(2,4),
∴m•22+2(m+2)+2=4,
解得m=- ,
,
∴抛物线解析式为y=- x2+
x2+ x+2,
x+2,
令y=0,则- x2+
x2+ x+2=0,
x+2=0,
整理得,x2-5x-6=0,
解得x1=-1,x2=6,
令x=0,则y=2,
∴A(-1,0),B(6,0),C(0,2),
过点B作BM⊥CD交CD的延长线于M,
在Rt△DOC中,∵OC=OD=2,
∴∠CDO=∠BDM=45°,CD=2 ,
,
在Rt△BMD中,∵BD=6-2=4,
∴DM=BM=4×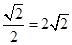 ,
,
在Rt△CMD中,tan∠BCM=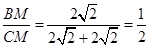 ,
,
又∵tan∠ACO=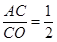 ,
,
∴∠ACO=∠BCD;
(2)①由勾股定理得,BC=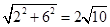 ,
,
BE=DE时,点E的横坐标为6-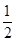 ×(6-2)=4,点E的纵坐标是
×(6-2)=4,点E的纵坐标是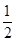 ×(6-2)×
×(6-2)×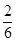 =
=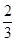 ,
,
所以,点E1(4,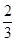 );
);
BE=BD时,点E的横坐标为6-(6-2)×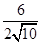 =6-
=6-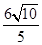 ,点E的纵坐标为(6-2)×
,点E的纵坐标为(6-2)×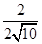 =
=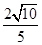 ,
,
所以,点E2(6-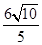 ,
,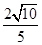 ),
),
综上所述,点E1(4,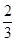 );或E2(6-
);或E2(6-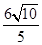 ,
,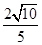 )时,△BDE是等腰三角形;
)时,△BDE是等腰三角形;
②设P(x,- x2+
x2+ x+2),
x+2),
过点P作x轴的垂线,垂足为F,交CD的延长线于点Q,
则直线CD的解析式为y=-x+2,
∴点Q(x,-x+2),
S△CDP=S△CPQ-S△DPQ,=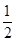 PQ•OF-
PQ•OF-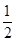 PQ•DF=
PQ•DF=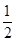 PQ•OD,
PQ•OD,
∵OD=2,
∴S△CDP=PQ=- x2+
x2+ x+2-(-x+2)=-
x+2-(-x+2)=- x2+
x2+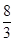 x(0<x<6),
x(0<x<6),
∵S=- x2+
x2+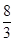 x=-
x=- (x-4)2+
(x-4)2+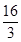 ,
,
∴当x=4时,△CDP的面积最大,
此时,- x2+
x2+ x+2=-
x+2=- ×42+
×42+ ×4+2=
×4+2=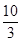 ,
,
∴点P(4,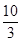 ),
),
设直线PD的解析式为y=kx+b(k≠0),
∴ 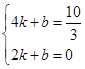 ,
,
解得  ,
,
∴直线PD的解析式为y= x-
x-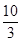 ,
,
直线BC的解析式为y=- x+2,
x+2,
联立 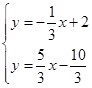 ,
,
解得 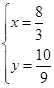 ,
,
所以,点E的坐标为( ,
,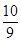 ).
).
考点: 二次函数综合题.


 x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
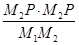 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由. 经过A(
经过A( ,0)、B(5,0)两点,顶点为P.
,0)、B(5,0)两点,顶点为P. ,
, )和点D(
)和点D( ,
, )在该抛物线上,则当
)在该抛物线上,则当 时,
时,
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).

 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少? (k为正整数).
(k为正整数).
 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数