题目内容
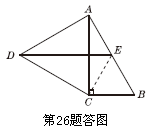
如图所示,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接DE.
(1)证明:DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.


分析:(1)根据∠BCD=90°+60°=150°,因此只要证明∠EDC=30°即可.根据已知条件及图形的位置关系,连接CE,通过证明△ADE≌△CDE,得到∠EDC=30°,所以∠EDC+∠DCB=180°,从而证得DE∥CB.
(2)此题可通过假设四边形DCBE是平行四边形,求出AC与AB的数量关系.
(1)证明:如图所示,连接CE,
∵ E为Rt△ACB的斜边AB的中点,
∴ CE=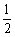 AB=AE.
AB=AE.
 ∵ △ACD是等边三角形,∴ AD=CD.
∵ △ACD是等边三角形,∴ AD=CD.
在△ADE和△CDE中,AD=CD,DE=DE,AE=CE,
∴ △ADE≌△CDE(SSS).∴ ∠ADE=∠CDE=30°.
∵ ∠DCB=∠ACB+∠ACD=90°+60°=150°,
∴ ∠EDC+∠DCB=180°,∴ DE∥CB.
(2)解:∵ ∠DCB=150°,
若四边形DCBE是平行四边形,
则DC∥BE,∠DCB+∠B=180°,∴ ∠B=30°.
在Rt△ACB中,AC= 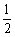 AB或AB=2AC.
AB或AB=2AC.
∴ 当AC=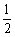 AB或AB=2AC时,四边形DCBE是平行四边形.
AB或AB=2AC时,四边形DCBE是平行四边形.
点拨:(1)利用直角三角形中,斜边上的中线等于斜边的一半进行转化,说明线段相等是证明两个三角形全等的关键;(2)对于条件探索性问题常通过逆向思维的方式得到解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 平面直角坐标系中,
平面直角坐标系中,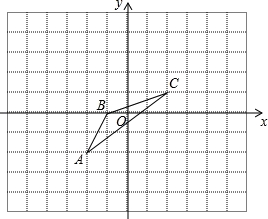
 时,
时, =_____________.
=_____________.  的周长是
的周长是 ,底边
,底边 上的高
上的高 的长是4,求这个三角形各边的长.
的长是4,求这个三角形各边的长.
 ; D.2(x-1)=3x-5
; D.2(x-1)=3x-5 的值互为相反数,那么x= 。
的值互为相反数,那么x= 。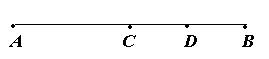
 AB-BD ;D. CD=
AB-BD ;D. CD= AB
AB