题目内容
【题目】如图，在平面直角坐标系xOy中，△OA1B1绕点O逆时针旋转90°，得△OA2B2；△OA2B2绕点O逆时针旋转90°，得△OA3B3；△OA3B3绕点O逆时针旋转90°，得△OA4B4；…；若点A1（1,0），B1（1,1），则点B4的坐标是________，点B 2018的坐标是________．
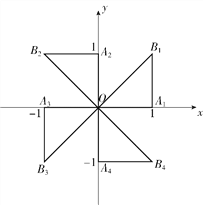
【答案】 点B4的坐标是（1,﹣1）， 点B2018的坐标是（﹣1,1）．
【解析】
根据旋转的性质结合题目中的已知条件进行分析计算得到点B2、B3、B4的坐标，并由此找到点Bn的坐标在旋转过程中的变化规律即可.
∵点A1、B1的坐标分别为（1，0）、（1，1），
∴OA1=1，A1B1=1，
由旋转的性质可得：OA4=OA3=OA2=OA1=1，A4B4=A3B3=A2B2=A1B1=1，
∴B2的坐标为（-1，1）、B3的坐标为（-1，-1）、B4的坐标为（1，-1），
∵
，
∴点B2018与点B2重合，
∴点B2018的坐标为（-1，1）.
故答案为：（1）（1，-1）；（2）（-1，1）.
练习册系列答案
阅读快车系列答案
相关题目
