Question

如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

(1)折叠后，DC的对应线段是       ，CF的对应线段是         ；
(2)若∠1=50°，求∠2、∠3的度数；
(3)若AB=7，DE=8，求CF的长度。

Answer 1

（1）折叠后，DC的对应线段是BC′，CF的对应线段是C′F；
（2）∠2=∠BEF，
∴∠3=80°；
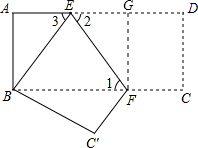
（3）FC =．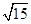

解析试题分析：(1）确定对应关系即可解决；
（2）∠2=∠BEF．由AD∥BC得∠1=∠2，所以∠2=∠BEF=50°，从而得∠3=80°；
（3）过点F作FG⊥AD于点G，在△ABE中，解出AE，得出EG的长，进而根据FC=GD=DE-EG即可得出答案．
考点：翻折变换（折叠问题）；全等三角形的判定与性质；矩形的性质．
点评：此题有一定的难度，需要综合运用折叠的性质及勾股定理，注意相等线段之间的代换．