题目内容
平行四边形ABCD中，E是BC中点，F是BE中点，AE与DF交于H，则AH：HE=________．
4
分析：首先根据平行四边形ABCD中，E是BC中点，F是BE中点，易知EF=
AD．再利用平行四边形的性质证得△DAH∽△FEH，再根据
相似三角形的性质，求得AH：HE的值．
解答：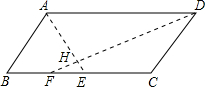
解：∵E是BC中点，F是BE中点，
∴EF=BC=AD，
∵平行四边形ABCD中，
∴∠DAH=∠FEH，∠ADH=∠EFH，
∴△DAH∽△FEH，
∴
=4，
即AH：HE=4．
故答案为：4．
点评：本题考查相似三角形的判定与性质、平行四边形的性质．解决本题的关键是熟练运用相似三角形的判定与性质定理．
分析：首先根据平行四边形ABCD中，E是BC中点，F是BE中点，易知EF=
AD．再利用平行四边形的性质证得△DAH∽△FEH，再根据相似三角形的性质，求得AH：HE的值．
解答：
解：∵E是BC中点，F是BE中点，∴EF=
BC=AD，∵平行四边形ABCD中，
∴∠DAH=∠FEH，∠ADH=∠EFH，
∴△DAH∽△FEH，
∴
=4，即AH：HE=4．
故答案为：4．
点评：本题考查相似三角形的判定与性质、平行四边形的性质．解决本题的关键是熟练运用相似三角形的判定与性质定理．
练习册系列答案
相关题目
如图，在平行四边形ABCD中，高h=4，则平行四边形ABCD的面积S=
如图，在平行四边形ABCD中，AE：EB=1：2，S△AEF=3，则S△FCD=
如图，在平行四边形ABCD中，E是BD上一点，AE的延长线交DC于点F，交BC的延长线于点G．求证：
如图，在平行四边形ABCD中，E、F分别是AD、BC的中点，AC分别交BE、DF于G、H，下列结论：
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．