题目内容
(8分)在□ABCD中，E、F分别是AB、CD的中点，连接AF、CE．
(1)求证：△BEC≌△DFA；
(2)连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．
证明：（1）∵四边形ABCD是平行四边形
∴AB=CD，∠B=∠D，BC=AD
∵E、F分别是AB、CD的中点
∴BE=
AB，DF=CD
∴BE=DF
∴△BEC≌△DFA
（2）四边形AECF是梯形。
∵四边形ABCD是平行四边形，
∴AB∥CD且AB=CD。
∵E、F分别是AB、CD的中点
∴AE=AB，CF=CD
∴AE∥CF且AE=CF。
∵CA=CB，E是AB的中点，
∴CE⊥AB，即∠AEC=90°
∴
AECF是矩形。
解析:略
练习册系列答案
相关题目
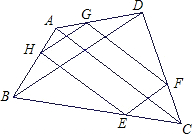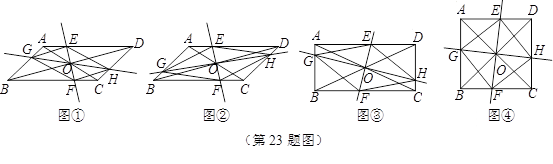
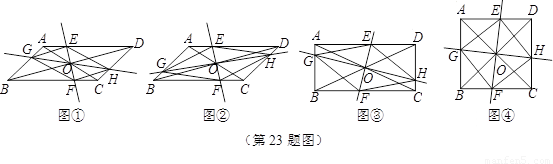
在四边形ABCD中，AC、BD是四边形ABCD的两条对角线，点E、F、G、H分别是在四边形ABCD的四边上的动点，但E、F、G、H不与A、B、C、D重合，且EF∥BD∥GH，FG∥AC∥HE．
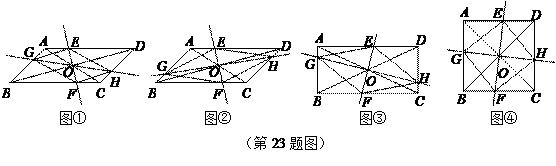
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.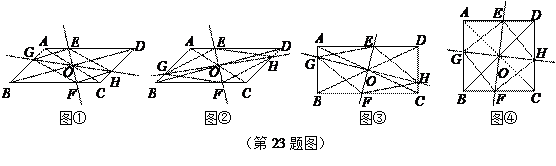
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.
在 ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.