题目内容

如图，△ABC是边长为1的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S₁；取BE中点E₁，作E₁D₁∥FB，E₁F₁∥EF，得到四边形E₁D₁FF₁，它的面积记作S₂．照此规律作下去，S₂₀₁₂=

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：先根据△ABC是等边三角形可求出△ABC的高，再根据三角形中位线定理可求出S₁的值，进而可得出S₂的值，找出规律即可得出S₂₀₁₂的值．
解答：∵△ABC是边长为1的等边三角形，
∴△ABC的高=AB•sinA=1× $\text{[math]}$ = $\text{[math]}$ ，
∵DE、EF是△ABC的中位线，
∴AF= $\text{[math]}$ ，
∴S₁= $\text{[math]}$ × $\text{[math]}$ × $\text{[math]}$ = $\text{[math]}$ ；
同理可得，S₂= $\text{[math]}$ × $\text{[math]}$ ；
…
∴S_n= $\text{[math]}$ ×（ $\text{[math]}$ ）^n-1；
∴S₂₀₁₂= $\text{[math]}$ ×（ $\text{[math]}$ ）²⁰¹¹= $\text{[math]}$ ．
故选D．
点评：本题考查的是相似多边形的性质，涉及到等边三角形的性质、锐角三角函数的定义、特殊角的三角函数值及三角形中位线定理，熟知以上知识是解答此题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

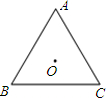如图，△ABC是边长为a的等边三角形，O为△ABC的中心．将△ABC绕着中心O旋转120°．
①直接写出△ABC的内切圆半径r和外接圆半径R分别是多少？
②设点D、E、F分别在边AB、BC、CA上，且AD=2DB，BE=2EC，CF=2FA，试画出△DEF，说明它的形状，并计算它的周长；
③根据“线动成面”的道理，△ABC的三条边AB、BC和CA在旋转过程中扫过的部分组成的平面图形的形状是什么？并计算出此图形的面积．

（2012•遵义）如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与

点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（1）当∠BQD=30°时，求AP的长；
（2）当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

（2013•溧水县一模）如图，△ABC是边长为4的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连结BD，交AC于F．
（1）猜想BD与DE的位置关系，并证明你的结论；
（2）求△BDE的面积S．

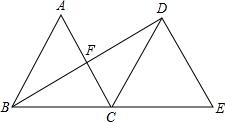（2012•湘潭）如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F．
（1）猜想AC与BD的位置关系，并证明你的结论；
（2）求线段BD的长．

如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120°，以D为顶点做一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为