题目内容
如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 在第一象限的图象交于
在第一象限的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知△
,已知△![]() 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点![]() 与点
与点![]() 不重合),
不重合),
且![]() 点的横坐标为1,在
点的横坐标为1,在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 最小.
最小.

解:(1) 设A点的坐标为(![]() ,
,![]() ),则
),则![]() .∴
.∴ ![]() .
.
∵ ![]() ,∴
,∴ ![]() .∴
.∴ ![]() .
.
∴ 反比例函数的解析式为![]() .
.
(2) 由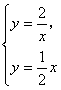 得
得![]() 或
或![]() ∴ A为
∴ A为![]() .
.
设A点关于![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为![]() .
.
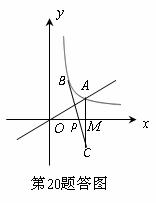
如要在![]() 轴上求一点P,使PA+PB最小,即
轴上求一点P,使PA+PB最小,即![]() 最小,则P点应为BC
最小,则P点应为BC
和x轴的交点,如图所示.
令直线BC的解析式为![]() .
.
∵ B为(![]() ,
,![]() ),∴
),∴![]() ∴
∴![]()
∴ BC的解析式为![]() .
.
当![]() 时,
时,![]() .∴ P点坐标为
.∴ P点坐标为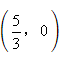 .
.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图,正比例函数
如图,正比例函数 OC的面积是24,且cos∠AOC=
OC的面积是24,且cos∠AOC= 已知:如图,正比例函数的图象经过点P和点Q(-m,m+3),求m的值.
已知:如图,正比例函数的图象经过点P和点Q(-m,m+3),求m的值. 如图,正比例函数
如图,正比例函数 与二次函数y=-x2+2x+c的图象都经过点A(2,m).
与二次函数y=-x2+2x+c的图象都经过点A(2,m). 与二次函数y=-x2+2x+c的图象都经过点A(2,m).
与二次函数y=-x2+2x+c的图象都经过点A(2,m).