题目内容
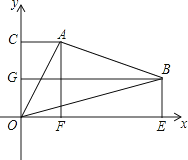
【题目】在平面直角坐标系xOy中，有一个边长为2个单位长度的等边△ABC，满足AC∥y轴．平移△ABC得到△A′B′C′，使点A′、B′分别在x轴、y轴上（不包括原点），则此时点C′的坐标是．.
【答案】（ 
,2）或（ ,-2）或（- ,2）或（- ,-2）
【解析】①如图1，B在AC左边；
C′在第一象限，点C′的坐标是（ ，2）；
C′在第四象限，点C′的坐标是（ ，-2）；
②B在AC右边；
C′在第二象限，点C′的坐标是（- ，2）；
C′在第三象限，点C′的坐标是（- ，-2）．
故点C′的坐标是（ ，2）或（ ，-2）或（- ，2）或（- ，-2）．
【考点精析】掌握坐标确定位置是解答本题的根本，需要知道对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标．
练习册系列答案
相关题目
