题目内容
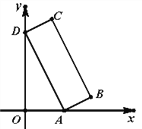
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() .对角线
.对角线![]() 相交于点
相交于点![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,分别与
,分别与![]() 交于点
交于点![]() .
.
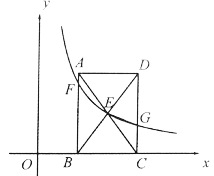
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)k=20;(2)△CEG的面积为![]() .
.
【解析】
(1)先利用矩形的性质和线段中点坐标公式得到E(5,4),然后把E点坐标代入![]() 可求得k的值;
可求得k的值;
(2)利用勾股定理计算出AC=10,则BE=EC=5,所以BF=7,设OB=t,则F(t,7),E(t+3,4),利用反比例函数图象上点的坐标得到7t=4(t+3),解得t=4,从而得到反比例函数解析式为y=![]() ,然后确定G点坐标,最后利用三角形面积公式计算△CEG的面积.
,然后确定G点坐标,最后利用三角形面积公式计算△CEG的面积.
(1)∵在矩形ABCD的顶点B,AB=8,BC=6,
而OC=8,
∴B(2,0),A(2,8),C(8,0),
∵对角线AC,BD相交于点E,
∴点E为AC的中点,
∴E(5,4),
把E(5,4)代入y=![]() 得k=5×4=20;
得k=5×4=20;
(2)∵AC=![]() =10,
=10,
∴BE=EC=5,
∵BF﹣BE=2,
∴BF=7,
设OB=t,则F(t,7),E(t+3,4),
∵反比例函数y=![]() (x>0)的图象经过点E、F,
(x>0)的图象经过点E、F,
∴7t=4(t+3),解得t=4,
∴k=7t=28,
∴反比例函数解析式为y=![]() ,
,
当x=10时,y=![]() ,
,
∴G(10,![]() ),
),
∴△CEG的面积=![]() .
.

练习册系列答案
相关题目