题目内容
如图,PA、PB分别与⊙O相切于A、B两点,且OP=2,∠APB=60.若点C在⊙O上,且AC= ,则圆周角∠CAB的度数为_______.
,则圆周角∠CAB的度数为_______.
15 75
解析试题分析;∵PA PB 是⊙0的切线 ∴∠PAO="∠PBO=90" 又∠APB="60" ∴∠APO="∠BPO=30" ∴∠AOP="∠BOP=60" ∠AOB=120  ∴AO="BO=1" (在直角三角形中,30度的角所对的边等于斜边的一半,)又AC= AO="1" ,∴点C有两种情况在AB的优弧和劣弧上。∴求得角为15° 75°
∴AO="BO=1" (在直角三角形中,30度的角所对的边等于斜边的一半,)又AC= AO="1" ,∴点C有两种情况在AB的优弧和劣弧上。∴求得角为15° 75°
考点:圆切线的性质,及优(劣)弧的定义。及直角三角形特殊角与边的关系。
点评:熟练掌握切线定理,在直角三角形中由特殊的角的三边关系,得到所求。本题有两个答案,易漏掉,属于中档题,有一定的难度。

练习册系列答案
相关题目
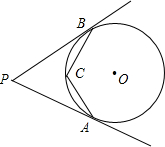 如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB=
如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB= 7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )
7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ) 7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是
7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 (2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.
(2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 如图,PA,PB分别切⊙O于点A和点B,C是
如图,PA,PB分别切⊙O于点A和点B,C是