题目内容
初次见面通常以握手示礼,适当的握手时间与力度会让人有一种舒服亲切的感受.某次联谊会有41人参加,若41位与会人员彼此握手一次,那么全体与会人员共握手
n(n-1)
n(n-1)次.
820
820
次.如果有n个人参加,那么全体与会人员共握手| 1 |
| 2 |
| 1 |
| 2 |
分析:设握手x次,根据图表中给出的类比规律,可知当有n个人时,握手次数为
n(n-1),根据此规律可求出握手次数.
| 1 |
| 2 |
解答:解:由题意得:设握手n次,则
x=
n(n-1),
当n=41时,x=
n(n-1)=
×41×(41-1)=820.
故答案为:820,
n(n-1).
x=
| 1 |
| 2 |
当n=41时,x=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:820,
| 1 |
| 2 |
点评:本题考查理解题意的能力,关键根据图表给的信心找出握手总次数和人数的关系式,从而可列出方程求解.

练习册系列答案
相关题目
【附加题】初次见面通常以握手示礼,适当的握手时间与力度会让人有一种舒服亲切的感受.某次联谊会有41人参加,若41位与会人员彼此握手一次,那么全体与会人员共握手多少次?其实要解决这个问题,可以作以下的分析:假若用点来表示每个人,连接两点的线段数目表示握手的次数,则结合表中提示,根据发现的规律,解决题中提出的问题.
| 握手图标 | 握手人数 | 握手次数 |
 |
2 | 1 |
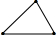 |
3 | 3 |
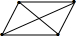 |
4 | 6 |
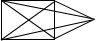 |
5 | 10 |
| … | … | … |