题目内容
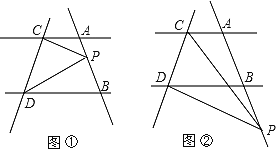
【题目】如图,![]() 是
是![]() 的外角,
的外角,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
(2)探索![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)80、40;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]() .
.
【解析】
(1)由三角形内角和定理可求∠A,然后求出∠OBC和∠OCD,再由三角形外角的性质即可求出结论;
(2)由题中角平分线可得∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACD,根据三角形内角和定理可得∠A+∠ABO=∠O+∠ACO,又由∠ACD=∠A+∠ABC=∠A+2∠ABO,进而得出∠A+∠ABO=∠O+
∠ACD,根据三角形内角和定理可得∠A+∠ABO=∠O+∠ACO,又由∠ACD=∠A+∠ABC=∠A+2∠ABO,进而得出∠A+∠ABO=∠O+![]() ∠A+∠ABO,即可得出结论;
∠A+∠ABO,即可得出结论;
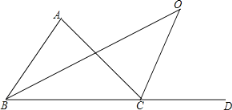
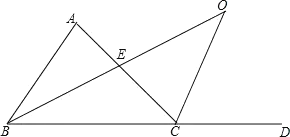
(3)AC与BO交于点E,由OC∥AB,证得∠ABO=∠O,由AC⊥BO,证得∠AEB=90°,故2∠O+∠O=90°,进而证得∠A=60°,由∠ABC=2∠ABO即可证得结论.
设![]() 与
与![]() 交于点
交于点![]()
解:(1)![]() ,
,![]() ,
,![]() ,
,
![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
故答案为:80、40;
(2)∵BO平分∠ABC,
∴∠ABO=![]() ∠ABC,
∠ABC,
∵CO平分∠ACD,
∴∠ACO=![]() ∠ACD,
∠ACD,
∵∠AEB=∠CEO,
∴∠A+∠ABO=∠O+∠ACO,
∴∠A+∠ABO=∠O+![]() ∠ACD,
∠ACD,
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC=∠A+2∠ABO,
∴∠A+∠ABO=∠O+![]() ∠A+∠ABO,
∠A+∠ABO,
∴![]() ∠A=∠O;
∠A=∠O;
(3)如图,![]() 与
与![]() 交于点
交于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小明根据学习函数的经验,对函数y=|x|+2的图象与性质进行了研究,下面是小明的研究过程,请补充完成.
(1)函数y=|x|+2的自变量x的取值范围是 ;
(2)列表,把表格填写完整:
x | …… | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
|
|
|
|
| …… |
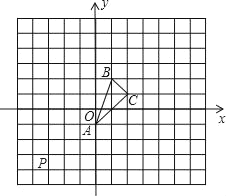
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的两条性质.