题目内容

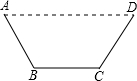
如图，在矩形ABCD中，AB=a，BC=b，
b
3
≤a≤3b，AE=AH=CF=CG，则四边形EFGH的面积的最大值是（　　）
A．
1
16
(a+b)2		B．
1
8
(a+b)2		C．
1
4
(a+b)2		D．
1
2
(a+b)2

设AE=AH=CF=CG=x，则BE=DG=a-x，BF=DH=b-x，
设四边形EFGH的面积为y，
依题意，得y=ab-x2-（a-x）（b-x），
即：y=-2x2+（a+b）x，
∵-2＜0，抛物线开口向下，
函数有最大值为
-(a+b)2
4×(-2)
=
1
8
（a+b）2．
故选B．
练习册系列答案
相关题目
对于任意两个二次函数：y1=a1x2+b1x+c1，y2=a2x2+b2x+c2，（a1a2≠0），当|a1|=|a2|时，我们称这两个二次函数的图象为全等抛物线．
现有△ABM，A（-1，0），B（1，0）．记过三点的二次函数抛物线为“C□□□”（“□□□”中填写相应三个点的字母）
（1）若已知M（0，1），△ABM≌△ABN（0，-1）．请通过计算判断CABM与CABN是否为全等抛物线；
（2）在图2中，以A、B、M三点为顶点，画出平行四边形．
①若已知M（0，n），求抛物线CABM的解析式，并直接写出所有过平行四边形中三个顶点且能与CABM全等的抛物线解析式．
②若已知M（m，n），当m，n满足什么条件时，存在抛物线CABM根据以上的探究结果，判断是否存在过平行四边形中三个顶点且能与CABM全等的抛物线？若存在，请列出所有满足条件的抛物线“C□□□”；若不存在，请说明理由．
抛物线y=（x-3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．

（1）求点B及点D的坐标．
（2）连结BD，CD，抛物线的对称轴与x轴交于点E．
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．
有一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m．
（1）在如图所示的直角坐标系中，求出该抛物线的解析式；
（2）设正常水位时桥下的水深为2m，为保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水深超过多少米时就会影响过往船只在桥下的顺利航行．
如图，抛物线y=ax2-5ax+4经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC，过A、B、C三点的抛物线的解析式为______．
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3}，函数y=-x的“特征数”是{0，-1，0}
（1）将“特征数”是{1，-4，1}的函数的图象向下平移2个单位，得到一个新函数图象，求这个新函数图象的解析式；
（2）“特征数”是{0，-
3
3
，
3
}的函数图象与x、y轴分别交点C、D，“特征数”是{0，-
3
，
3
}的函数图象与x轴交于点E，点O是原点，判断△ODC与△OED是否相似，请说明理由．
已知某种水果的批发单价与批发量的函数关系如图1所示．
（1）请说明图中①、②两段函数图象的实际意义；
（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在图2的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果；
（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图3所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．
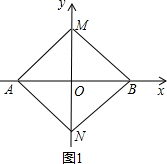
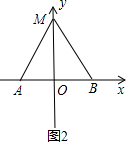
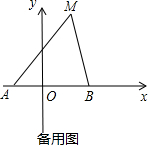
如图，已知抛物线y=x2-2x+n与x轴交于不同的两点A，B，其顶点是C，D是抛物线的对称轴与x轴的交点．
（1）求实数n的取值范围．
（2）求顶点C的坐标；
（3）求线段AB的长；
（4）若直线y=
2
x+1分别交x轴于E，交y轴于F，问△BDC与△EOF是否有可能全等？如果有可能全等请给出证明；如果不可能全等请说明理由．
现有一个长为2米的长方形铁片，要把它制成一个开口的水槽．
（1）方案甲，如果做成一个底边长为1米，两边高都为0.5米开口长方形水槽，求水槽的横截面面积．
（2）方案乙，如图把铁片制成等腰梯形水槽，使∠ABC=∠BCD=120°．设BC=2xcm，梯形ABCD（水槽的横截面）的面积为ycm2，试写出y关于x的函数关系式以及自变量x的取值范围，并求出y的最大值；
（3）你能找到一种使水槽的横截面面积比方案乙中的y更大的设计方案吗？若能，请画出图形，标出必要的数据（可不写解答过程），写出你所设计方案的横截面面积；若不能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网