题目内容
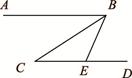
如图，AB∥CD，AD平分∠BAC，∠C=80°，则∠D的度数为( )。
| A．50° | B．55° | C．70° | D．80° |
A.
解析试题分析：∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵AB∥CD，
∴∠BAD=∠D，
∴∠CAD=∠D，
在△ACD中，∠C+∠D+∠CAD=180°，
∴80°+∠D+∠D=180°，
解得∠D=50°．
故选A．
考点: 1.平行线的性质；2.角平分线的定义．
练习册系列答案
阅读快车系列答案
相关题目
，则∠BED 的度数是（ ）
下列命题是真命题的有（ ）
①对角线相等的四边形是矩形；②两直线平行，同位角相等；③若AO=OB，则点O是AB的中点；④对角线相等的梯形是等腰梯形；⑤平分弦的直径垂直于弦，并且平分弦所对的弧。
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，AB∥EF，∠C=90°，则α、β、γ的关系为（ ）
| A．β=α+γ | B．α+β+γ=180° | C．β+γ-α=90° | D．α+β-γ=90° |
如图，已知AB∥CD，∠2=135°，则∠1的度数是
| A．35° | B．45° | C．55° | D．65° |
如图，直线a、b被直线c所截，下列说法正确的是（ ）
| A．当∠1＝∠2时，一定有a∥b |
| B．当a∥b时，一定有∠1＝∠2 |
| C．当a∥b时，一定有∠1＋∠2＝90° |
| D．当∠1＋∠2＝180°时，一定有a∥b |
如图，AC⊥BC，AD⊥CD，AB＝a，CD=b，则AC的取值范围是（ ）
| A．大于b | B．小于a |
| C．大于b且小于a | D．无法确定 |
过平面上
三点中的任意两点作直线，可作( )
| A．1条 | B．3条 | C．1条或3条 | D．无数条 |