题目内容
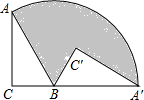 将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是________.
将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A在同一直线上,则阴影部分的面积是________.
 π-2
π-2
分析:根据勾股定理可求AC的长,根据三角函数的知识可得∠ABC的度数,从而得到扇形圆心角的度数,阴影部分的面积=扇形面积-△A′BC′的面积,由此即可求解.
解答:∵在Rt△ACB中,∠C=90°,AB=4,BC=2,
∴AC=
 =2
=2 ,cos∠ABC=
,cos∠ABC= ,
,∴∠ABC=60°,
∴∠ABA′=120°,
由旋转的性质可得A′C′=AC=2
 ,BC′=BC=2,
,BC′=BC=2,∴阴影部分的面积是:
 -
- ×2×2
×2×2 =
= π-2
π-2 .
.故答案为:
 π-2
π-2 .
.点评:本题考查了扇形面积的计算,解题的关键是得到扇形圆心角的度数.

练习册系列答案
相关题目
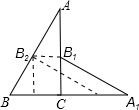 如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )
如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )A、(3π+3-
| ||||
B、(3π-3+
| ||||
C、(
| ||||
D、(
|
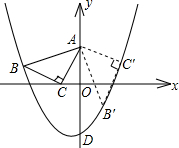 中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).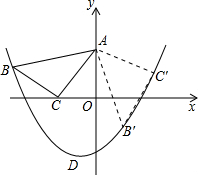 ,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上.
,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上. 将Rt△ABC绕顶点C分别旋转90°、180°、270°得到图所示的图形,连接BB1、B1B2、B2B3、B3B,已知直角边BC=1,求四边形BB1B2B3的形状及其面积.
将Rt△ABC绕顶点C分别旋转90°、180°、270°得到图所示的图形,连接BB1、B1B2、B2B3、B3B,已知直角边BC=1,求四边形BB1B2B3的形状及其面积.