Question

已知四条直线y=mx-3，y=1，y=3，和x=1所围的面积是12，求m的值．

Answer 1

分析：先画出四条直线，直线x=1与直线y=1，y=3的交点分别为A（1，1），B（1，3）；直线y=mx-3与y=1，y=3的交点分别为D（

4

m

，1），C（

6

m

，3）；然后讨论m＞0，或m＜0，分别表示出AD和BC的长，用直角梯形的面积建立方程，解方程可得到m的值．

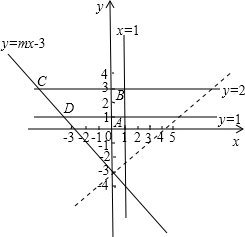解答：解：如图，
则A（1，1），B（1，3），C（

6

m

，3），D（

4

m

，1），AB=2，四边形ABCD为直角梯形，
当m＜0，则BC=1-

6

m

，AD=1-

4

m

，
S_{直角梯形ABCD}=

1

2

×AB×（BC+AD）=12，
所以

1

2

•2•（1-

6

m

+1-

4

m

）=12，
方程转化为：

1

m

=-1，解得m=-1，经检验是原方程的解．
所以m=-1；
当m＞0，则BC=

6

m

-1，AD=

4

m

-1，
所以

1

2

•2•（

6

m

-1+

4

m

-1）=12，
方程转化为：

5

m

=7，解得m=

5

7

，经检验是原方程的解．
所以m=

5

7

．
故所求的m的值为-1或

5

7

．

点评：本题考查了一次函数y=kx+b（k≠0，k，b为常数）的性质．它的图象为一条直线，当k＞0，图象经过第一，三象限，y随x的增大而增大；当k＜0，图象经过第二，四象限，y随x的增大而减小；当b＞0，图象与y轴的交点在x轴的上方；当b=0，图象过坐标原点；当b＜0，图象与y轴的交点在x轴的下方．也考查了直线交点的坐标的求法．