题目内容
（2012•聊城）如图，⊙O是△ABC的外接圆，AB=AC=10，BC=12，P是 | BC |
（1）当点P在什么位置时，DP是⊙O的切线？请说明理由；
（2）当DP为⊙O的切线时，求线段DP的长．
分析：（1）根据当点P是
的中点时，得出
=
，得出PA是○O的直径，再利用DP∥BC，得出DP⊥PA，问题得证；
（2）利用切线的性质，由勾股定理得出半径长，进而得出△ABE∽△ADP，即可得出DP的长．
|
| BC |
|
| PBA |
|
| PCA |
（2）利用切线的性质，由勾股定理得出半径长，进而得出△ABE∽△ADP，即可得出DP的长．
解答：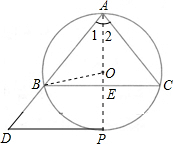
解：（1）当点P是
的中点时，DP是⊙O的切线．理由如下：
∵AB=AC，
∴
=
，
又∵
=
，
∴
=
，
∴PA是⊙O的直径，
∵
=
，
∴∠1=∠2，
又AB=AC，
∴PA⊥BC，
又∵DP∥BC，
∴DP⊥PA，
∴DP是⊙O的切线．
（2）连接OB，设PA交BC于点E．
由垂径定理，得BE=
BC=6，
在Rt△ABE中，由勾股定理，得：
AE=
=
=8，
设⊙O的半径为r，则OE=8-r，
在Rt△OBE中，由勾股定理，得：
r2=62+（8-r）2，
解得r=
，
∵DP∥BC，∴∠ABE=∠D，
又∵∠1=∠1，
∴△ABE∽△ADP，
∴
=
，即
=
，
解得：DP=
．
解：（1）当点P是 |
| BC |
∵AB=AC，
∴
|
| AB |
|
| AC |
又∵
|
| PB |
|
| PC |
∴
|
| PBA |
|
| PCA |
∴PA是⊙O的直径，
∵
|
| PB |
|
| PC |
∴∠1=∠2，
又AB=AC，
∴PA⊥BC，
又∵DP∥BC，
∴DP⊥PA，
∴DP是⊙O的切线．
（2）连接OB，设PA交BC于点E．
由垂径定理，得BE=
| 1 |
| 2 |
在Rt△ABE中，由勾股定理，得：
AE=
| AB2-BE2 |
| 102-62 |
设⊙O的半径为r，则OE=8-r，
在Rt△OBE中，由勾股定理，得：
r2=62+（8-r）2，
解得r=
| 25 |
| 4 |
∵DP∥BC，∴∠ABE=∠D，
又∵∠1=∠1，
∴△ABE∽△ADP，
∴
| BE |
| DP |
| AE |
| AP |
| 6 |
| DP |
| 8 | ||
2×
|
解得：DP=
| 75 |
| 8 |
点评：此题主要考查了切线的判定与性质以及勾股定理和相似三角形的判定与性质，根据已知得出△ABE∽△ADP是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
（2012•聊城）如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是（ ）
（2012•聊城）如图，四边形ABCD是平行四边形，点E在边BC上，如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是（ ）
（2012•聊城）如图，在直角坐标系中，以原点O为圆心的同心圆的半径由内向外依次为1，2，3，4，…，同心圆与直线y=x和y=-x分别交于A1，A2，A3，A4…，则点A30的坐标是（ ）
（2012•聊城）如图，在直角坐标系中，正方形的中心在原点O，且正方形的一组对边与x轴平行，点P（3a，a）是反比例函数y=
（2012•聊城）如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．