题目内容
如图1,四边形ABCD,AEFG都是正方形,E、G分别在AB、AD边上,已知AB=4.
(1)求正方形ABCD的周长;
(2)将正方形AEFG绕点A逆时针旋转![]() (
(![]() )时,如图
)时,如图![]() 2,
2,
求证:BE=DG.
(3)将正方形AEFG绕点A逆时针旋转45°时,如图3,延长BE交DG于点H,
设BH与AD的交点为M.
①求证:BH⊥DG;
②当AE=![]() 时,求线段BH的长(精确到0.1).
时,求线段BH的长(精确到0.1).
![]()



(1)16 2分
(2)∵四边形ABCD,AEFG都是正方形
∴AB=AD,AE=AG,∠BAE=∠DAG=![]() 3分
3分
∴△BAE≌△DAG 4分
∴BE=DG 5分
(3)①∵△BAE≌△DAG ∴∠ABE=∠ADG 6分
又∠AMB=∠DMH ∴∠DHM=∠BAM=90°
∴BH⊥DG 7分
②连结GE交AD于点N.
∵AEFG是正方形, ∴AF与EG互相垂直平分
∴AN=GN=1 ∴DG=![]() 8分
8分
法一:连结DE
S△DEG=![]() GE·ND=
GE·ND=![]() DG·HE 10分
DG·HE 10分
∴HE=![]() 11分
11分
∵EB=DG=![]()
∴BH=BE+HE=![]() +
+![]() ≈5.1 12分
≈5.1 12分
法二: 连结BD,BG
S四边形ABDG=S△BDG+S△ABG=S△ADG+S△ABD 10分
∴![]() DG·BH+
DG·BH+![]() AB·NA=
AB·NA=![]() AD·GN+
AD·GN+![]() AB·AD 11分
AB·AD 11分
∴BH=![]() ≈5.1 12分
≈5.1 12分

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
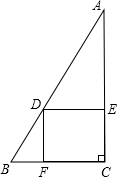 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.