Question

已知二次函数y=x²-x-2及实数a＞-2，求
（1）函数在一2＜x≤a的最小值；
（2）函数在a≤x≤a+2的最小值．

Answer 1

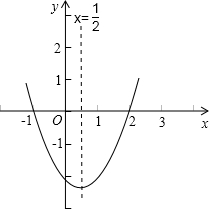
解：二次函数y=x²-x-2=-的图象如图：
顶点坐标为（，），
（1）当-2＜a＜时，函数为减函数，
最小值为当x=a时，y=a²-a-2．
当a≥时，y_min=-，

（2）当a＞-2，且a+2＜，
即：-2＜a＜-时，函数为减函数，
最小值为：y_x=a+2=（a+2）²-（a+2）-2，
当a＜≤a+2，即-≤a＜时，
函数的最小值为y=-．
分析：已知二次函数y=x²-x-2，（1）根据函数解析式画出函数的大致图象，找出顶点坐标，根据图象具体分析当实数a＞-2及一2＜x≤a时得出此时x的取值范围即可得出y的最小值，（2）当a≤x≤a+2及a＞-2得出此时x的取值范围，即可得出y的最小值．
点评：本题考查了二次函数的最值，难度较大，关键是题中要根据a的取值范围分析得出x的取值范围，再得出y的最小值．