题目内容
抛物线y=ax2-4ax+b经过A(1,0),F(4,-3),与y轴交于点C,与x轴交于另一点B.(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,连接PC,将线段PC绕着P点逆时针旋转90°至线段PC1,使得C1落在抛物线上?若存在,求点P的坐标;若不存在,请说明理由;
(3)点D是抛物线在x轴上方部分的一点,过D作DE∥AC与y轴交于E,且四边形ACED是等腰梯形,求出D的坐标.
分析:(1)将A、F两点坐标代入抛物线解析式可求a、b的值,确定抛物线解析式;
(2)由(1)可知,抛物线对称轴为x=2,设P(2,t)利用垂直关系构造两个三角形全等,可得C1(t+5,t-2),将C1点坐标代入抛物线解析式求t即可;
(3)延长DA交y轴于点M,由等腰梯形构造等腰三角形,可得MA=MC,在Rt△AOM中,由勾股定理求OM,根据A、M两点坐标求直线AD解析式,与抛物线解析式联立,求D点坐标.
(2)由(1)可知,抛物线对称轴为x=2,设P(2,t)利用垂直关系构造两个三角形全等,可得C1(t+5,t-2),将C1点坐标代入抛物线解析式求t即可;
(3)延长DA交y轴于点M,由等腰梯形构造等腰三角形,可得MA=MC,在Rt△AOM中,由勾股定理求OM,根据A、M两点坐标求直线AD解析式,与抛物线解析式联立,求D点坐标.
解答:解:(1)把A(1,0),F(4,-3)代入y=ax2-4ax+b中,
得
,
解得
,
∴y=-x2+4x-3;
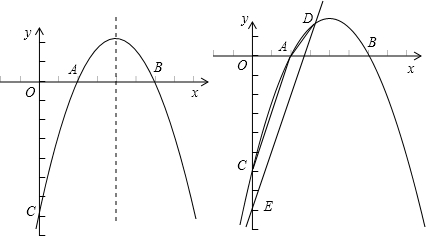
(2)如图1,设P(2,t),
分别过C、C′作对称轴的垂线,垂足为G、H,
∵PC=PC′,∠CPC′=90°,由互余关系可证△PCG≌△C′PH,
∴PH=CG=2,HC′=PG=t+3,
则C1(t+5,t-2),代入y=-x2+4x-3中,得
t-2=-(t+5)2+4(t+5)-3,
解得t=-1或t=-6.
∴P(2,-1)或P(2,-6)
(3)如图2,延长DA交y轴于点M,依题意,
∠CED=∠ADE,MD=ME,则MA=MC,
在Rt△AOM中,OM2+OA2=AM2,即OM2+12=(3-OM)2,
解得OM=
,
∴直线DA的解析式是y=
x-
,
联立
,
解得
或
,
∴D(
,
)

得
|
解得
|
∴y=-x2+4x-3;
(2)如图1,设P(2,t),
分别过C、C′作对称轴的垂线,垂足为G、H,
∵PC=PC′,∠CPC′=90°,由互余关系可证△PCG≌△C′PH,
∴PH=CG=2,HC′=PG=t+3,
则C1(t+5,t-2),代入y=-x2+4x-3中,得
t-2=-(t+5)2+4(t+5)-3,
解得t=-1或t=-6.
∴P(2,-1)或P(2,-6)
(3)如图2,延长DA交y轴于点M,依题意,
∠CED=∠ADE,MD=ME,则MA=MC,
在Rt△AOM中,OM2+OA2=AM2,即OM2+12=(3-OM)2,
解得OM=
| 4 |
| 3 |
∴直线DA的解析式是y=
| 4 |
| 3 |
| 4 |
| 3 |
联立
|
解得
|
|
∴D(
| 5 |
| 3 |
| 8 |
| 9 |

点评:本题考查了二次函数的综合运用.关键是根据已知条件求抛物线解析式,由互余关系,旋转的性质构造全等三角形,由等腰梯形构造等腰三角形,体现了转化的思想.

练习册系列答案
相关题目
已知点(2,8)在抛物线y=ax2上,则a的值为( )
| A、±2 | ||
B、±2
| ||
| C、2 | ||
| D、-2 |
若(2,0)、(4,0)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线( )
| A、x=0 | B、x=1 | C、x=2 | D、x=3 |


 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.