Question

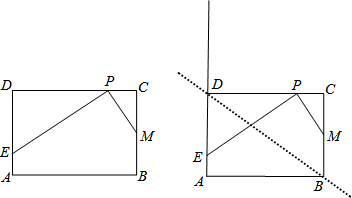
已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）。连接PM，过点P作PM的垂线与射线DA相交于点E（如图）。设CP=x，DE=y。

（1）写出y与x之间的函数关系式        ；

（2）若点E与点A重合，则x的值为        ；

（3）是否存在点P，使得点D关于直线PE的对称点D′落在边AB上？若存在，求x的值；若不存在，请说明理由。

Answer 1

解：（1）y=－x²＋4x。

            （2）或。

            （3）存在。

                 过点P作PH⊥AB于点H。则

                 ∵点D关于直线PE的对称点D′落在边AB上，

                 ∴P D′=PD=4－x，E D′=ED= y=－x²＋4x，EA=AD－ED= x²－4x＋2，∠P D′E=∠D=90⁰。

                 在Rt△D′P H中，PH=2， D′P =DP=4－x，D′H=。

                 ∵∠ E D′A=180⁰－90⁰－∠P D′H=90⁰－∠P D′H=∠D′P H，∠P D′E=∠P HD′ =90⁰，

                 ∴△E D′A∽△D′P H。∴，即，

  即，两边平方并整理得，2x²－4x＋1=0。解得。

∵当时，y=，

∴此时，点E已在边DA延长线上，不合题意，舍去（实际上是无理方程的增根）。

∵当时，y=，

∴此时，点E在边AD上，符合题意。

∴当时，点D关于直线PE的对称点D′落在边AB上。