题目内容
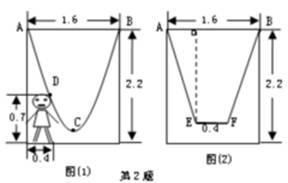
如图①，单杠高为2.2 m，两柱之间的距离为1.6 m，将一根绳子的两端系在立柱与铁杆AB结合处，绳子自然下垂呈近似抛物线形状．
(1)一身高0.7 m的小孩站在离立柱0.4 m处，其头部刚好接触在绳子上，求绳子的最低点C到地面的距离；
(2)为供孩子们荡秋千，把绳子剪断后，中间系一块长0.4 m的木板，除掉系木板用去的绳子后，两边的绳长正好各为2 m，木板与地面平行(如图②)，求这时木板到地面的距离．
(参考数据：
≈1.8，
≈1.9，
≈2.1，精确到0.1 m．)
答案：
解析：
解析：
(1)以AB的中垂线为y轴，以地面为x轴建立坐标系．设二次函数的解析式为y＝ax2＋c，将D(－0.4，0.7)，B(0.8，2.2)代入解析式中，可得y＝3.125x2＋0.2．
(2)分别作EG⊥AB于G，FH⊥AB于H．则AG0.6，由勾股定理，得EG＝
≈1.9，∴2.2－1.9＝0.3，∴木板到地面的距离约为0.3 m．
练习册系列答案
相关题目
如图所示，一单杠高2.2m，两立柱间的距离为1.6m，将一根绳子的两端拴于立柱与铁杠的结合处A、B，绳子自然下垂，虽抛物线状，一个身高0.7m的小孩站在距立柱0.4m处，其头部刚好触上绳子的D处，求绳子的最低点O到地面的距离．
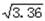≈1.8，
≈1.9，
≈2.1)．
≈1.8, 
≈1.9, 
≈2.1).
≈1.8，
≈1.9，
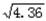≈2.1）。