题目内容
在一个不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外完全相同,将球摇匀,从中任取1球.
(1)请按取出不同颜色球的概率从小到大的顺序排列;
(2)怎样改变各颜色球的数目,使取出每一种颜色的球的概率相等.
解:(1)根据题意,袋子中共6个球,其中有1个白球,2个黄球和3个红球,故将球摇匀,从中任取1球,
①恰好取出白球的可能性为 ,
,
②恰好取出黄球的可能性为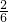 =
= ,
,
③恰好取出红球的可能性为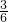 =
= ,
,
故这些事件按发生的可能性从小到大的顺序排列是①<②<③.
(2)将其中一个红球变成白球,可使取出每种颜色的球的概率都相等.此题答案不唯一.
分析:(1)根据可能性大小的求法,求出各个事件发生的可能性的大小,再按照大小顺序从小到大排列起来即可.
(2)由于袋子中有三种颜色的6个球,要从袋子中随机取出一个球,使取出每种颜色的球的概率都相等,可知每一种球的概率都是 ,据此不难得出一个方案.
,据此不难得出一个方案.
点评:本题主要考查了可能性大小计算,即概率的计算方法,用到的知识点为:可能性等于所求情况数与总情况数之比,难度适中.
①恰好取出白球的可能性为
 ,
,②恰好取出黄球的可能性为
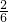 =
= ,
,③恰好取出红球的可能性为
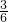 =
= ,
,故这些事件按发生的可能性从小到大的顺序排列是①<②<③.
(2)将其中一个红球变成白球,可使取出每种颜色的球的概率都相等.此题答案不唯一.
分析:(1)根据可能性大小的求法,求出各个事件发生的可能性的大小,再按照大小顺序从小到大排列起来即可.
(2)由于袋子中有三种颜色的6个球,要从袋子中随机取出一个球,使取出每种颜色的球的概率都相等,可知每一种球的概率都是
 ,据此不难得出一个方案.
,据此不难得出一个方案.点评:本题主要考查了可能性大小计算,即概率的计算方法,用到的知识点为:可能性等于所求情况数与总情况数之比,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目