题目内容
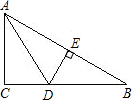 已知:如图,在Rt△ABC中,∠C=90°,∠BAD=
已知:如图,在Rt△ABC中,∠C=90°,∠BAD=| 1 |
| 2 |
| 1 |
| 2 |
分析:由条件先证△BED≌△AED,得,∠B=∠2=∠1,再根据直角三角形的性质,两锐角的和为90°,求得∠B=30°即可得证.
解答: 解:∵DE⊥AB,
解:∵DE⊥AB,
∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠3=∠4,又∵DE=DE,
∴△BED≌△AED(ASA),
∴AD=BD,∠2=∠B,
∵∠BAD=∠2=
∠BAC,
∴∠1=∠2=∠B,
∵AD=BD,∠1+∠2+∠B=90°,
∴∠B=∠1=∠2=30°,
在直角三角形ACD中,∠1=30°,
∴CD=
AD=
BD.
 解:∵DE⊥AB,
解:∵DE⊥AB,∴∠AED=∠BED=90°,
∵DE是∠ADB的平分线,
∴∠3=∠4,又∵DE=DE,
∴△BED≌△AED(ASA),
∴AD=BD,∠2=∠B,
∵∠BAD=∠2=
| 1 |
| 2 |
∴∠1=∠2=∠B,
∵AD=BD,∠1+∠2+∠B=90°,
∴∠B=∠1=∠2=30°,
在直角三角形ACD中,∠1=30°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题利用了:①全等三角形的判定和性质,②直角三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
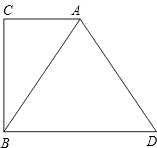 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.