Question

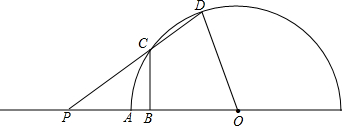
已知：半圆O的半径OA=4，P是OA延长线上一点，过线段OP的中点B作垂线交⊙O于点C，射线PC交⊙O于点D，连接OD．
（1）若，求弦CD的长．
（2）若点C在上时，设PA=x，CD=y，求y与x的函数关系式及自变量x的取值范围；
（3）设CD的中点为E，射线BE与射线OD交于点F，当DF=1时，请直接写出tan∠P的值．

Answer 1

【答案】分析：（1）根据，得出∠DOC=∠AOC，进而求出PC=OC，以及△DOC∽△DPO，再利用相似三角形的性质得出即可；
（2）作OE⊥CD，求出△PBC∽△PEO，进而得出=，即可求出y与x的关系式；
（3）分别利用若点D在外部时，以及利用若点D在上时，利用等腰三角形的性质以及锐角三角函数关系得出tan∠P的值即可．
解答：解：（1）连接OC，如图1，
∵，
∴∠DOC=∠AOC，
又∵BC垂直平分OP，
∴PC=OC，
而OA=4，
∴CP=OC=4，
∴∠P=∠POC，
∴∠CPO=∠COD，
而∠PDO=∠ODC，
∴△DOC∽△DPO，
∴DC：OD=OD：DP，即OD²=DC•DP，
∴DC（DC+4）=16，
∴CD=2-2；

（2）作OE⊥CD，垂足为E，如图1，
则CE=CD=y，
∵∠P=∠P，∠PBC=∠PEO=90°，
∴△PBC∽△PEO，
∴=，
而PB=OP=（x+4），PE=PC+CE=4+y，
∴，
∴y=x²+2x-4（4-4＜x＜4）；

（3）若点D在外部时，
连接OC和OE．
显然可以得：Rt△CBP≌Rt△CBO，
∴∠CPB=∠COB=x（不妨设其大小为x）
∴∠DCO=2x．（三角形外角的性质定理），
同时，PC=OC=R=4，
∵CE=DE（已知）
∴由垂径定理可知：OE⊥CD，
在△Rt△OEC和Rt△OED中，
∵，
∴Rt△OEC≌Rt△OED （SSS）
∴∠ODC=∠OCD=2x．
同时，由锐角三角函数定义，
在Rt△OPE中．
tan∠APD=，
∵∠CBO=∠CEO=90°，
∴四点B，C，E，O四点共圆，
∴由同圆中，同弧上的圆周角相等可知
∠BEC=∠BOC=x，
∴∠DEF=∠BEC（对顶角相等）=∠BOC=x．
在△DEF中，由三角形外角性质定理，
∠ODC=∠F+∠DEF，
∴2x=∠F+x，
∴∠F=x．
∴△DEF为等腰三角形，
CE=DE=DF=1．
∴PE=PC+CE=4+1=5，
在Rt△ODE中，DE=1，OD=R=4，
∴由勾股定理可得OE=，
∴tan∠P==，
若点D在上时，
同理可知 CE=DE=DF=1，PC=OC=r=4，
故PE=3，OE=，
则tan∠P==．
点评：此题主要考查了圆的综合应用以及全等三角形的判定与性质以及勾股定理和四点共圆以及等腰三角形的性质等知识，利用数形结合以及分类讨论得出是解题关键．