题目内容
如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OA和OC是方程x2-(3+| 3 |
| 3 |
(1)求线段OA和OC的长;
(2)求点D的坐标;
(3)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存
 在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
分析:(1)通过解答题目中的一元二次方程的根就是OA、OC的长.
(2)由折纸可以知道CD=OC,从而求出AD,作DF⊥OA于F解直角三角形可以求出D点的坐标.
(3)存在满足条件的M点,利用三角形全等和平行线等分线段定理可以求出M点对应的坐标.
(2)由折纸可以知道CD=OC,从而求出AD,作DF⊥OA于F解直角三角形可以求出D点的坐标.
(3)存在满足条件的M点,利用三角形全等和平行线等分线段定理可以求出M点对应的坐标.
解答: 解:(1)解方程x2-(3+
解:(1)解方程x2-(3+
)x+3
=0得:
x1=
,x2=3
∵OA>OC
∴OA=3,OC=
;
(2)在Rt△AOC中,由勾股定理得:
AC=2
由轴对称得:CO=CD=
∴AD=
,作DF⊥OA,且∠CAO=30°
∴DF=
,由勾股定理得:
AF=
∴OF=
,∴OF=AF
∴D(
,
);
(3)∵M1N1∥AC,
∠N1M1F=∠ADF,∠FN1M1=∠FAD
∵OF=AF
∴△ADF≌△N1M1F(AAS),
∴M1F=DF=
,N1F=AF=
∴M1(
,-
),作MG⊥OA,
∵四边形MCDN和四边形CN1M1D是平行四边形
∴MC=ND,ND=CM1
∴MC=CM1
∴GO=OF=
,OE=1
∴GE=
∴EOC△∽△EGM
∴
=
∴
=
解得:
MG=
∴M(-
,
)
 解:(1)解方程x2-(3+
解:(1)解方程x2-(3+| 3 |
| 3 |
x1=
| 3 |
∵OA>OC
∴OA=3,OC=
| 3 |
(2)在Rt△AOC中,由勾股定理得:
AC=2
| 3 |
由轴对称得:CO=CD=
| 3 |
∴AD=
| 3 |
∴DF=
| ||
| 2 |
AF=
| 3 |
| 2 |
∴OF=
| 3 |
| 2 |
∴D(
| 3 |
| 2 |
| ||
| 2 |
(3)∵M1N1∥AC,
∠N1M1F=∠ADF,∠FN1M1=∠FAD
∵OF=AF
∴△ADF≌△N1M1F(AAS),
∴M1F=DF=
| ||
| 2 |
| 3 |
| 2 |
∴M1(
| 3 |
| 2 |
| ||
| 2 |
∵四边形MCDN和四边形CN1M1D是平行四边形
∴MC=ND,ND=CM1
∴MC=CM1
∴GO=OF=
| 3 |
| 2 |
∴GE=
| 5 |
| 2 |
∴EOC△∽△EGM
∴
| EO |
| GE |
| CO |
| MG |
∴
| 1 | ||
|
| ||
| MG |
MG=
5
| ||
| 2 |
∴M(-
| 3 |
| 2 |
5
| ||
| 2 |
点评:本题是一道一次函数的综合试题,考查了一元二次方程的根,待定系数法求函数的解析式、勾股定理、全等三角形的性质,平行四边形的性质,相似三角形的运用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
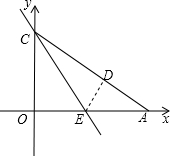 A在x轴上,点C在y轴上,OC=
A在x轴上,点C在y轴上,OC= 如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=
如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC= ,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
 ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.