题目内容
函数y=
(k为常数)的图象经过点(-1,-2),当x>0时,y随着x的增大而
| x | k |
减小
减小
.(填增大或减小)分析:利用待定系数法求得k的值,然后根据k的符号来判定该函数的单调性.
解答:解:∵函数y=
(k为常数)的图象经过点(-1,-2),
∴-2=
,
解得,k=
>0;
∴函数y=2x的图象位于第一、三象限,且在每一象限内y随着x的增大而减小;
故答案是:减小.
| x |
| k |
∴-2=
| -1 |
| k |
解得,k=
| 1 |
| 2 |
∴函数y=2x的图象位于第一、三象限,且在每一象限内y随着x的增大而减小;
故答案是:减小.
点评:本题考查了待定系数法求反比例函数的解析式、反比例函数的性质.反比例函数y=
的图象,当k>0时,在每个象限内,y随x的增大而减小.
| x |
| k |

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
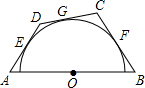 如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在
如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在 |
| EF |
| A、正比例函数y=kx(k为常数,k≠0,x>0) | ||
| B、一次函数y=kx+b(k,b为常数,kb≠0,x>0) | ||
C、反比例函数y=
| ||
| D、二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0) |
 (2012•成都)如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数
(2012•成都)如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数