题目内容
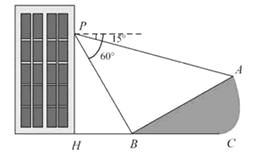
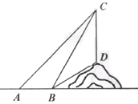
【题目】如图，小山坡上有一根垂直于地面的电线杆
，小明从地面上的A处测得电线杆顶端
点的仰角是45°,后他正对电线杆向前走6米到达B处，测得电线杆顶端点和电线杆底端D点的仰角分别是60°和30°.求电线杆的高度（结果保留根号）
【答案】CD= 
【解析】
延长CD交AB于点E，设DE=x，在直角△BDE和直角△BCE中，根据30°角的直角三角形的性质利用x表示出CE和BE，根据等腰直角三角形得AE=CE即可列出方程求得x的值，根据CD=CE-DE即可求得CD的长度．
解：如图，延长CD交AB于点E ，
∵∠DBE=30°∴设DE=x,则BE=
，
∵∠CBE=60°∴CE=
∵∠CBE=45°则
解得：
∴ CD=CE-DE=2
.
故答案为：CD= .
练习册系列答案
相关题目
