题目内容
如图所示,已知正方形 的面积为9 ,点
的面积为9 ,点 在函数
在函数 的图象上,点
的图象上,点 (
( )是函数
)是函数 的图象上动点,过点
的图象上动点,过点 分别作
分别作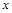 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,若设矩形
,若设矩形 和正方形
和正方形 不重合的两部分的面积和为
不重合的两部分的面积和为 。
。
(1)求
 点坐标和
点坐标和 的值;(2)写出
的值;(2)写出 关于
关于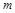 的函数关系和
的函数关系和 的最大值。
的最大值。
(1)∵正方形OABC的面积为9,
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数 的图象上的一点,
的图象上的一点,
∴ ,
,
∴k=9; 3分
(2)分两种情况:
若点P在点B的右侧,如图(1),
则PE=n,AE=m﹣3,
∴S= ;
;
若点P在点B的左侧,如图(2),
则PF=m,FC=n﹣3,
∴S= ;
;
 的最大值为9. 6分解析:
的最大值为9. 6分解析:
(1)由于点B在函数y= 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
(2)分类讨论阴影部分(矩形)的面积。
∴正方形OABC的边长为3,即OA=3,AB=3,
∴B点坐标为(3,3).
又∵点B是函数
 的图象上的一点,
的图象上的一点,∴
 ,
,∴k=9; 3分
(2)分两种情况:
若点P在点B的右侧,如图(1),
则PE=n,AE=m﹣3,
∴S=
 ;
;若点P在点B的左侧,如图(2),
则PF=m,FC=n﹣3,
∴S=
 ;
; 的最大值为9. 6分解析:
的最大值为9. 6分解析:(1)由于点B在函数y=
 的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;
的图象上,而正方形OABC的面积为9,由此可以得到正方形边长为3,接着得到B的坐标及k的值;(2)分类讨论阴影部分(矩形)的面积。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 33、如图所示,已知正方形ABCD,延长CB至E,连接AE,过点A作AF⊥AE交DC于F.
33、如图所示,已知正方形ABCD,延长CB至E,连接AE,过点A作AF⊥AE交DC于F. 30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,
30、如图所示,已知正方形ABCD,E为BC上任意一点,延长AB至F,使BF=BE,AE的延长线交CF于G,
 如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( )
如图所示,已知正方形ABCD的面积是8平方厘米,正方形EFGH的面积是62平方厘米,BC落在EH上,△ACG的面积是4.9平方厘米,则△ABE的面积是( ) 如图所示,已知正方形OABC的面积为9,点B在函数
如图所示,已知正方形OABC的面积为9,点B在函数