题目内容
如图，P是等腰直角△ABC内一点，BC是斜边，如果将△ABP绕点A按逆时针方向旋转到△ACP′的位置，则∠APP′的度数为
- A.30°
- B.45°
- C.50°
- D.60°
B
分析：首先根据旋转可知∠1=∠2，AP=AP′，再求出∠PAP′=90°，可得到△APP′是等腰直角三角形，进而求出∠APP′的度数．
解答：
解：∵将△ABP绕点A按逆时针方向旋转到△ACP′的位置，
∴∠1=∠2，AP=AP′，
∵∠CAB=90°，
即：∠2+∠CAP=90°，
∴∠1+∠CAP=90°，
∴△APP′是等腰直角三角形，
∴∠APP′=45°．
故选：B．
点评：此题主要考查了等腰直角三角形的判定，旋转的性质，解决问题的关键是证明∠PAP′=90°．
分析：首先根据旋转可知∠1=∠2，AP=AP′，再求出∠PAP′=90°，可得到△APP′是等腰直角三角形，进而求出∠APP′的度数．
解答：
解：∵将△ABP绕点A按逆时针方向旋转到△ACP′的位置，∴∠1=∠2，AP=AP′，
∵∠CAB=90°，
即：∠2+∠CAP=90°，
∴∠1+∠CAP=90°，
∴△APP′是等腰直角三角形，
∴∠APP′=45°．
故选：B．
点评：此题主要考查了等腰直角三角形的判定，旋转的性质，解决问题的关键是证明∠PAP′=90°．
练习册系列答案
相关题目
如图，△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于（ ）A、3
| ||
B、2
| ||
C、4
| ||
D、3
|
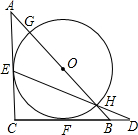如图，△ABC是等腰直角三角形，AC=BC=a，以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F，与AB分别相交于点G、H，且EH的延长线与CB的延长线交于点D，则CD的长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
22、已知如图，△ABC是等腰直角三角形，∠C为直角．
如图，△A1A2B是等腰直角三角形，∠A1A2B=90°，A2A3⊥A1B，垂足为A3，A3A4⊥A2B，垂足为A4，A4A5⊥A3B，垂足为A5，…，An+1An+2⊥AnB，垂足为An+2（n为正整数），若A1A2=A2B=a，则线段An+1An+2的长为（ ）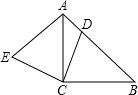
已知：如图，△ABC是等腰直角三角形，D为斜边AB上任意一点（不与A，B重合），连接CD，作EC⊥DC，且EC=DC，连接AE．