题目内容
证明:(a+b+c)2+a2+b2+c2=(a+b)2+(b+c)2+(a+c)2.
证明:(a+b+c)2+a2+b2+c2=[(a+b)+c]2+a2+b2+c2,
=(a+b)2+2(a+b)c+c2+a2+b2+c2,
=(a+b)2+2ac+2bc+c2+a2+b2+c2,
=(a+b)2+(a2+2ac+c2)+(b2+2bc+c2),
=(a+b)2+(a+c)2+(b+c)2.
分析:根据完全平方公式:(a±b)2=a2±2ab+b2变形求解.把等号左边是式子展开后重新组合,整理为等号右边的式子.
点评:本题考查了完全平方公式,整体思想的利用比较关键.
=(a+b)2+2(a+b)c+c2+a2+b2+c2,
=(a+b)2+2ac+2bc+c2+a2+b2+c2,
=(a+b)2+(a2+2ac+c2)+(b2+2bc+c2),
=(a+b)2+(a+c)2+(b+c)2.
分析:根据完全平方公式:(a±b)2=a2±2ab+b2变形求解.把等号左边是式子展开后重新组合,整理为等号右边的式子.
点评:本题考查了完全平方公式,整体思想的利用比较关键.

练习册系列答案
相关题目
 22、如图,已知:点B,F,C,D在同一直线上,且FB=CD,AB∥ED,AC∥FE,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.
22、如图,已知:点B,F,C,D在同一直线上,且FB=CD,AB∥ED,AC∥FE,请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.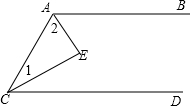 如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少?
如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少? 为半径作⊙O.
为半径作⊙O. 20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C
20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C