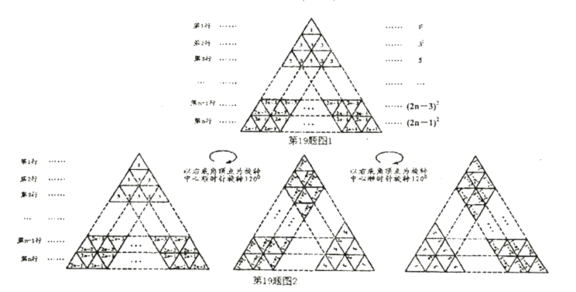
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijĪÄ»ÆÓĆĘ·ÉĢµź×¼±ø¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŹé°ü½ųŠŠĻśŹŪ£¬¾µ÷²é£¬ŅŅŹé°üµÄµ„¼Ū±Č¼×Źé°ü¹ó![]() ŌŖ£¬ÓĆ
ŌŖ£¬ÓĆ![]() ŌŖ¹ŗ½ųŅŅŹé°üµÄøöŹżÓėÓĆ
ŌŖ¹ŗ½ųŅŅŹé°üµÄøöŹżÓėÓĆ![]() ŌŖ¹ŗ½ų¼×Źé°üµÄøöŹżĻąµČ£®
ŌŖ¹ŗ½ų¼×Źé°üµÄøöŹżĻąµČ£®
£Ø1£©Ēó¼×”¢ŅŅĮ½ÖÖŹé°üµÄ½ų¼Ū·Ö±šĪŖ¶ąÉŁŌŖ?
£Ø2£©ÉĢ»§¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŹé°ü¹²![]() øö½ųŠŠŹŌĻś£¬ĘäÖŠ¼×Źé°üµÄøöŹż²»ÉŁÓŚ
øö½ųŠŠŹŌĻś£¬ĘäÖŠ¼×Źé°üµÄøöŹż²»ÉŁÓŚ![]() øö£¬ĒŅ¼×Źé°üµÄøöŹż µÄ
øö£¬ĒŅ¼×Źé°üµÄøöŹż µÄ![]() ±¶²»“óÓŚŅŅŹé°üµÄøöŹż£¬ŅŃÖŖ¼×Źé°üµÄŹŪ¼ŪĪŖ
±¶²»“óÓŚŅŅŹé°üµÄøöŹż£¬ŅŃÖŖ¼×Źé°üµÄŹŪ¼ŪĪŖ![]() ŌŖ/øö£¬ŅŅŹé°üµÄŹŪ¼ŪĪŖ
ŌŖ/øö£¬ŅŅŹé°üµÄŹŪ¼ŪĪŖ![]() ŌŖ/øö£¬ĒŅ Č«²æŹŪ³ö£¬Éč¹ŗ½ų¼×Źé°ü
ŌŖ/øö£¬ĒŅ Č«²æŹŪ³ö£¬Éč¹ŗ½ų¼×Źé°ü![]() øö£¬ĒóøĆÉĢµźĻśŹŪÕāÅśŹé°üµÄĄūČó
øö£¬ĒóøĆÉĢµźĻśŹŪÕāÅśŹé°üµÄĄūČó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢ Š“³ö
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢ Š“³ö![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©ŌŚ(2)µÄĢõ¼žĻĀ£¬øƵź½«![]() øöŹé°üČ«²æŹŪ³öŗó£¬Ź¹ÓĆĖł»ńµÄĄūČóÓÖ¹ŗ½ų
øöŹé°üČ«²æŹŪ³öŗó£¬Ź¹ÓĆĖł»ńµÄĄūČóÓÖ¹ŗ½ų![]() øöŹé°ü¾čŌłøų ʶĄ§µŲĒų¶łĶÆ£¬ÕāŃłøĆÉĢµźÕāÅśŹé°ü¹²»ńĄū
øöŹé°ü¾čŌłøų ʶĄ§µŲĒų¶łĶÆ£¬ÕāŃłøĆÉĢµźÕāÅśŹé°ü¹²»ńĄū![]() ŌŖ£®ĒėĒó³öøƵźµŚ¶ž“Ī½ų»õĖłŃ”ÓĆµÄ½ų»õ·½°ø?
ŌŖ£®ĒėĒó³öøƵźµŚ¶ž“Ī½ų»õĖłŃ”ÓĆµÄ½ų»õ·½°ø?
”¾“š°ø”æ£Ø1£©¼×Źé°ü½ų¼ŪĪŖ![]() ŌŖ,ŅŅŹé°ü½ų¼ŪĪŖ
ŌŖ,ŅŅŹé°ü½ų¼ŪĪŖ![]() ŌŖ£»£Ø2£©
ŌŖ£»£Ø2£©![]() £»£Ø3£©µŚ¶ž“Ī½ų»õ·½°øŹĒ¹ŗ½ų¼×Źé°ü
£»£Ø3£©µŚ¶ž“Ī½ų»õ·½°øŹĒ¹ŗ½ų¼×Źé°ü![]() øö£¬ŅŅŹé°ü
øö£¬ŅŅŹé°ü![]() øö£®
øö£®
”¾½āĪö”æ
£Ø1£©Éč¼×Źé°ü½ų¼ŪĪŖ![]() ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ
ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ![]() ŌŖ£¬øł¾Ż”°ÓĆ
ŌŖ£¬øł¾Ż”°ÓĆ![]() ŌŖ¹ŗ½ųŅŅŹé°üµÄøöŹżÓėÓĆ
ŌŖ¹ŗ½ųŅŅŹé°üµÄøöŹżÓėÓĆ![]() ŌŖ¹ŗ½ų¼×Źé°üµÄøöŹżĻąµČ”±ĮŠ·½³ĢĒó½ā¼“æÉ£»
ŌŖ¹ŗ½ų¼×Źé°üµÄøöŹżĻąµČ”±ĮŠ·½³ĢĒó½ā¼“æÉ£»
£Ø2£©øł¾ŻÉĢ»§¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŹé°ü¹²![]() øö½ųŠŠŹŌĻś£¬ĘäÖŠ¼×Źé°üµÄøöŹż²»ÉŁÓŚ
øö½ųŠŠŹŌĻś£¬ĘäÖŠ¼×Źé°üµÄøöŹż²»ÉŁÓŚ![]() øö£¬ĒŅ¼×Źé°üµÄøöŹż µÄ
øö£¬ĒŅ¼×Źé°üµÄøöŹż µÄ![]() ±¶²»“óÓŚŅŅŹé°üµÄøöŹżĒó³ömµÄȔֵ·¶Ī§£¬ŌŁøł¾ŻĄūČó”¢ŹŪ¼Ū”¢½ų¼ŪÓėĻśŹŪŹżĮæµÄ¹ŲĻµĮŠ³öŗÆŹż¹ŲĻµŹ½¼“æÉ£»
±¶²»“óÓŚŅŅŹé°üµÄøöŹżĒó³ömµÄȔֵ·¶Ī§£¬ŌŁøł¾ŻĄūČó”¢ŹŪ¼Ū”¢½ų¼ŪÓėĻśŹŪŹżĮæµÄ¹ŲĻµĮŠ³öŗÆŹż¹ŲĻµŹ½¼“æÉ£»
£Ø3£©øł¾ŻĢāÖŠµČĮæ¹ŲĻµĮŠ³ö·½³ĢĒó½ā¼“æÉ.
½ā:![]() Éč¼×Źé°ü½ų¼ŪĪŖ
Éč¼×Źé°ü½ų¼ŪĪŖ![]() ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ
ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ![]() ŌŖ
ŌŖ
øł¾ŻĢāŅā£¬µĆ![]()
½āµĆ![]()
¾¼ģŃé![]() ŹĒ·½³ĢµÄøł£¬ĒŅ·ūŗĻĢāŅā£¬Ōņ
ŹĒ·½³ĢµÄøł£¬ĒŅ·ūŗĻĢāŅā£¬Ōņ![]()
![]() ¼×Źé°ü½ų¼ŪĪŖ
¼×Źé°ü½ų¼ŪĪŖ![]() ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ
ŌŖ£¬ŅŅŹé°ü½ų¼ŪĪŖ![]() ŌŖ£®
ŌŖ£®
![]() ¹ŗ½ų¼×Źé°ü
¹ŗ½ų¼×Źé°ü![]() øö£¬
øö£¬
![]() ¹ŗ½ųŅŅŹé°ü
¹ŗ½ųŅŅŹé°ü![]() øö
øö
øł¾ŻĢāŅā£¬µĆ![]()
½āµĆ![]()
![]()
![]() ĒŅ
ĒŅ![]() ĪŖÕżÕūŹż£®
ĪŖÕżÕūŹż£®
![]()
![]() É赌¶ž“Ī¹ŗ½ų¼×Źé°ü
É赌¶ž“Ī¹ŗ½ų¼×Źé°ü![]() øö£¬Ōņ¹ŗ½ųŅŅŹé°ü
øö£¬Ōņ¹ŗ½ųŅŅŹé°ü![]() øö£®
øö£®
øł¾ŻĢāŅā£¬µĆ![]()
¼“![]()
![]() ĒŅ
ĒŅ![]() ĪŖÕżÕūŹż
ĪŖÕżÕūŹż
![]() µ±
µ±![]() Ź±£¬
Ź±£¬![]() ÓŠÕūŹż½ā
ÓŠÕūŹż½ā
![]() Ōņ
Ōņ![]()
![]() µŚ¶ž“Ī½ų»õ·½°øŹĒ¹ŗ½ų¼×Źé°ü
µŚ¶ž“Ī½ų»õ·½°øŹĒ¹ŗ½ų¼×Źé°ü![]() øö£¬ŅŅŹé°ü
øö£¬ŅŅŹé°ü![]() øö
øö