题目内容
若 与(b-27)2互为相反数,求
与(b-27)2互为相反数,求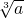 -
-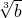 的立方根.
的立方根.
解:∵ 与(b-27)2互为相反数,
与(b-27)2互为相反数,
∴ +(b-27)2=0,
+(b-27)2=0,
而 ≥0,(b-27)2=0,
≥0,(b-27)2=0,
∴ =0,(b-27)2=0,
=0,(b-27)2=0,
∴a=-8,b=27,
∴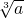 -
-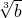 =-2-3=-5.
=-2-3=-5.
∴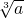 -
-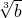 的立方根为
的立方根为 .
.
分析:由于 与(b-27)2互为相反数,那么它们的和为0,然后根据非负数的性质即可得到它们每一个等于0,由此即可得到关于a、b的方程,解方程即可求解.
与(b-27)2互为相反数,那么它们的和为0,然后根据非负数的性质即可得到它们每一个等于0,由此即可得到关于a、b的方程,解方程即可求解.
点评:此题主要考查了立方根的定义和非负数的性质,解题的关键是非负数的性质:如果几个非负数的和为0,那么每一个非负数都为0.
 与(b-27)2互为相反数,
与(b-27)2互为相反数,∴
 +(b-27)2=0,
+(b-27)2=0,而
 ≥0,(b-27)2=0,
≥0,(b-27)2=0,∴
 =0,(b-27)2=0,
=0,(b-27)2=0,∴a=-8,b=27,
∴
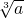 -
-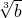 =-2-3=-5.
=-2-3=-5.∴
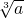 -
-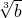 的立方根为
的立方根为 .
.分析:由于
 与(b-27)2互为相反数,那么它们的和为0,然后根据非负数的性质即可得到它们每一个等于0,由此即可得到关于a、b的方程,解方程即可求解.
与(b-27)2互为相反数,那么它们的和为0,然后根据非负数的性质即可得到它们每一个等于0,由此即可得到关于a、b的方程,解方程即可求解.点评:此题主要考查了立方根的定义和非负数的性质,解题的关键是非负数的性质:如果几个非负数的和为0,那么每一个非负数都为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目